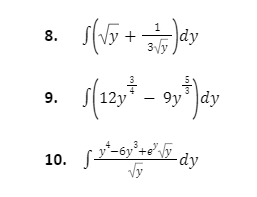Achieve your IIT dreams with Unacademy

Integration is used to address two fundamentally different types of things: The first class involves problems in which we know the function’s derivative, rate of change, or graph slope and wish to discover the function. As a result, we’ll have to reverse the differentiation process.

Integration Definition

In mathematics, integration is the process of finding a function g(x) whose derivative, Dg(x), is equal to a given function f(x).This is indicated by the integral sign “∫,” as in ∫f(x), commonly known as function’s indefinite integration.

Also explore: 

• JEE Main College Predictor 2024
• JEE Main 2024 Result Session 2

Types of integration

There are two types of integration:

1) Definite Integration and 2) Indefinite integration

Definite integration

the difference between the values of an integral for an upper value b and lower value a of the independent variable x for a particular function f(x).

A definite Integral is represented as:

An indefinite integral is one in which no limits are given and an arbitrary constant is added to the integral as a requirement.

A indefinite integration is represented as:

Example:

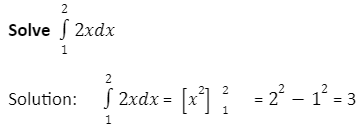
Relation between integration and differentiation

As far as we know, Differentiation and Integration are just opposite of each other.
Differentiation is the slope of any curve at any point x(say), while integration is the area under that same curve specified between two points, i.e. x1 and x2 (say).

Integration Basic formulae

1. ∫ 1 dx = x + C
2. ∫ a dx = ax+ C
3. ∫ x n dx = ((xn+1)/(n+1))+C ; n≠1
4. ∫ sin x dx = – cos x + C
5. ∫ sec2x dx = tan x + C
6. ∫ csc2x dx = -cot x + C
7. ∫ ex dx = ex+ C
8. ∫ a x dx = (a x/ln a) + C ; a>0,  a≠1
9. ∫1/√(1 – x2).dx = sin-1x + C
10. ∫ /1(1 – x2).dx = -cos-1x + C
11. ∫1/(1 + x2).dx = tan-1x + C
12. ∫ 1/(1 +x2 ).dx = -cot-1x + C
13. ∫ 1/x√(x2 – 1).dx = sec-1x + C
14. ∫1/(x2 – a2).dx = 1/2a.log|(x – a)(x + a| + C 
15. ∫ 1/(a2 – x2).dx =1/2a.log|(a + x)(a – x)| + C
16. ∫1/(x2 + a2).dx = 1/a.tan-1x/a + C
17. ∫1/√(x2 – a2)dx = log| x +√(x2 – a2)| + C
18. ∫ √(x2 – a2).dx =1/2.x.√(x2 – a2)-a2/2 log| x + √(x2 – a2)| + C 
19. ∫1/√(a2 – x2).dx = sin-1 x/a + C 
20. ∫√(a2 – x2).dx = 1/2.x.√(a2 – x2).dx + a2/2.sin-1 x/a + C
21. ∫1/√(x2 + a2 ).dx = log |x + √(x2 + a2)| + C 
22. ∫ √(x2 + a2 ).dx =1/2.x.√(x2 + a2 )+ a2/2 . log |x + √(x2 + a2 )| + C

Integration question examples

1.Integrate the following with respect to x  ∫ x11 dx

Solution :   

∫ x11 dx 

=  x (11 + 1)/(11 + 1) + c

=  (x12/12) + c

2.Integrate the following with respect to x   ∫ (1/x7) dx

Solution :

∫ (1/x7) dx =  ∫ x-7 dx 

=  x(-7 + 1)/(-7 + 1) + c

=  x-6/(-6) + c

=  (-1/6x6) + c

3.Integrate the following with respect to x   ∫ (tan x / cos x) dx

Solution :

∫(tan x / cos x) dx  =  ∫tan x  (1/cos x) dx

 =  ∫tan x  sec x dx

=  sec x + c

4.Integrate the following with respect to x   ∫ (cos x / sin2 x) dx

Solution :

∫(cos x / sin2 x) dx  =  ∫(cosx/sinx) (1/ sinx) dx

=  ∫cot x cosec x dx

=  – cosec x + c

5.Integrate the following with respect to x    ∫ (1 / cos2 x) dx

Solution :                                   

∫(1 / cos2 x) dx 

=  ∫ sec2 x dx

=  tan x + c

6.Integrate the following with respect to x    ∫ (x24/x25) dx

Solution :

∫ (x24/x25) dx  =  ∫ x24-25 dx

=  ∫ x-1 dx

=  ∫ (1/x) dx

=  log x + c

Indefinite integration for jee examples

1. Find the value of ∫2x cos (x2 – 5).

Solution: Let, I = ∫2xcos(x2 – 5).dx

Let x2 – 5 = t …..(1)

2x.dx = dt

Substituting these values, we have

I = ∫cos(t).dt

= sin t + c …..(2)

By giving the values of equation 1 into equation  2 , we get :

= sin (x2 – 5) + C

2.  ∫(xe+ex+ee) dx

Solution: I = ∫(xe+ex+ee) dx

Let us split the above equation.

∫xe dx + ∫ex dx + ∫ee dx

By the formula, we know;

∫xn dx = xn+1/n+1

Therefore,

xe+1/e+1 + ex + ee x + C

3.  Use the integration formula and find the value of 

∫(5 + 4Cosx)/Sin2x.dx

 ∫(5 + 4Cosx)/Sin2x.dx

= ∫5/Sin2x. dx +∫4Cosx/Sin2x.dx

= ∫5Cosec2x.dx + ∫4Cotx.Cosecx.dx

=5∫Cosec2x.dx + 4∫Cotx.Cosecx.dx

Using the trigonometric integration formula, we get

=5(-Cotx) + 4(-Cosecx)

= -5Cotx – 4Cosecx + C

Indefinite integration for JEE questions

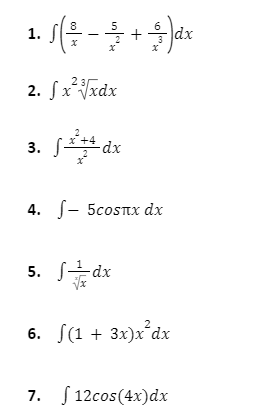
Conclusion

Multiple entities behaving as if they were a single entity to achieve common organisational goals should be conceived of as integration. Organizational structure, integrative processes, and organisational culture are all techniques that can be used to accomplish integration.