Profile
Settings
Refer your friends
Sign out
The area of an equilateral triangle refers to the amount of space it occupies in a two-dimensional plane. A triangle with all sides equal and all angles measuring 60 degrees is called an equilateral triangle. The number of unit squares that would fit into any two-dimensional shape is known as its area. The term “unit” refers to one (1), and a unit square is defined as a square having a side length of one unit. The area of an equilateral triangle, on the other hand, is the entire amount of space it encloses in a two-dimensional plane.
Area of Equilateral triangle:
The area of an equilateral triangle is defined as the area enclosed by the triangle’s three sides. It’s calculated in square units. in², m², cm², yd² and other key units are used to express the area of an equilateral triangle. In the sections below, we’ll look at the formula for calculating the area of an equilateral triangle and its derivation.
Formula: –
The area occupied between the sides of an equilateral triangle in a 2D plane is calculated using the equilateral triangle area formula. Many people use the ability to calculate the areas of any geometrical shape in their job. We have the formula for the area of an equilateral triangle. Finding the area of a triangle in a general triangle might be difficult for a variety of reasons. Finding the area of an equilateral triangle, on the other hand, is a simple computation.
The general formula for determining the area of a triangle whose base and height is known is given by:
Area = ½ × base × height
The area of an equilateral triangle is calculated using the following formula:
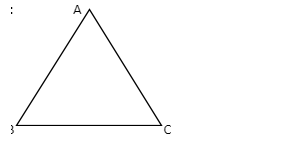
In the adjacent figure, AB = AC = BC = a cm.
So the area of the given equilateral triangle is given by:
A = √3/4 × (side)² sq. units
= √3/4 × a² cm²
Derivation of the formula
All of the sides of an equilateral triangle are equal, and all of the interior angles are 60 degrees. As a result, the area of an equilateral triangle can be calculated if one of the sides’ lengths is known. Using the formula, get the area of an equilateral triangle as,
Area = √3/4 × a² sq. units
Where, a = length of each side of the equilateral triangle.
The area of an equilateral triangle can be calculated using the method above in the following ways:
- Using the triangle’s general area:
The general area of the triangle formula can be used to generate the formula for calculating the area of an equilateral triangle. To accomplish so, we’ll need the lengths of each side and the equilateral triangle’s height. As a result, we’ll calculate an equilateral triangle’s height in terms of its side length.
The generic formula for the area of a triangle, which is equal to (½ × base × height), yields the formula for the area of an equilateral triangle. The formula for an equilateral triangle is deduced as follows.
Area of triangle = ½ × base × height
The Pythagoras theorem (hypotenuse² = base² + height²) is used
to find the height of the equilateral triangle.
Here, a/2 is the base, h is the height, and an is the hypotenuse.
(Refer to the figure aside)
Apply Pythagoras’ theorem to the triangle now.
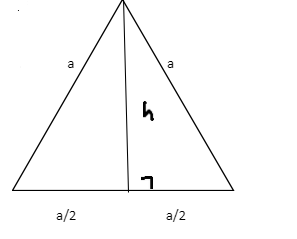
⇒ h² = a² – (a²/4)
⇒ h² = (3a²)/4.
Or, h = (√3a)/2
So the area of the triangle is given by ,
A = ½ × base × height
= ½ × a × (√3a)/2
= (√3/4)a²
Thus, the area of the equilateral triangle is given by (√3/4)a² .
- Using Heron’s formula
When the lengths of the triangle’s three sides are determined, Heron’s formula is used to calculate its area. Heron’s formula is named after Hero of Alexandria, a mathematician who can calculate the area of any triangle given the lengths of all three sides. When utilizing Heron’s formula to calculate the area of a triangle, we do not use angles or other distances.
The steps for calculating the area of a triangle are as follows:
Consider the ABC triangle, which has a, b, and c sides. The area of a triangle can be calculated using Heron’s formula, i.e., given by
A = √{S (S – a) (S – b) (S – c)}
Where, S is the semi-perimeter, which is calculated as follows:
S = (a+b+c)/2
But in case of equilateral triangle, a = b = c
So, S = (a + a + a)/2 = 3a/2
Hence the area is given by,
A = √{S (S – a) (S – a) (S – a)}
= √{3a/2(3a/2-a)³}
= √{3a/2 × a³/8}
= √(3a⁴/16)
= (√3/4)a² sq. units
Thus the area of the equilateral triangle is given by (√3/4)a² sq. units.
Conclusion:
The area of an equilateral triangle is defined as the area contained by the three sides of the triangle. It’s calculated in square units. The area of an equilateral triangle is commonly expressed in in², m², cm², and yd². The area of an equilateral triangle, the height of an equilateral triangle, the perimeter of an equilateral triangle, and the semi-perimeter of an equilateral triangle are all addressed here.
