Profile
Settings
Refer your friends
Sign out
The Basic Terms
The locus of point travelling at a fixed distance from a given point gives us a circle. The given point is often the centre of a circle or the fixed point. The distance between the fixed and the moving point is constant, tracing a circular path. Thus, the distance between the moving and fixed points is represented as the radius of a circle.
Infinite lines are passing through the circle that cut it into different sections. The line passing through the centre and intersecting on the boundary is the longest possible line inside the circle. This line is known as the diameter of the circle. Eventually, there can be many diameters. The radius and the diameter of the circle are linked as –
C=2πR or C=πD
Here, R is the radius,
D is the diameter, and
π is the mathematical constant used whose value is 22/7 or approximated at 3.14.
Now, the circumference of the circle can be used to evaluate the area of the circle.
Formula for Area of the Circle
The locus of a point concerning the fixed point creates a circle that is indeed a closed figure. The area can be evaluated for the closed figure, and thus, we can say that the area of the circle is the space enclosed by the circle’s boundary.
The radius of the circle can be used to compute the area. Hence, we have the area of the circle as –
Area =πR²
Thus, the area of the circle can be computed.
If the measurements of the diameter and/or circumference are given, then the formula for area of a circle can be evaluated as –
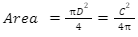
Problems Based on the Formula for Area of the Circle
Example 1 – The radius for the shape is measured. The value is 7 cm. Find the area of the shape if the given shape is a circle.
Solution –
The above shape is a circle having a radius of 7 cm.
We need to evaluate the area of the figure.
Thus, we can say that the area is –
Area = πR”=π7²=154 cm²
Example 2 – The cake is baked on a pan such that different sizes can be yielded. The pan can cover 100 cm2. For the cake to cover 75% of the area of the pan, what is the radius of the cake?
Solution –
The pan can cover a maximum area of 100 cm2. Thus, for the cake to cover 75% of the total area of the pan, the area covered by the cake is –
Area covered by the cake = 75% of 100 cm²=75 cm2
Now, the cake is circular in shape, as the pan is also circular. Thus, the radius of the cake can be evaluated as –
Area=πR²
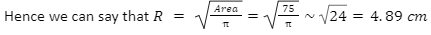
Thus, the radius of the cake, which would cover 75% of the pan, would be 4.89 cm approximately.
Example 3- A cricket field is covered by a fence. The total fences required were 100 of length 10 cm each. Evaluate the total space enclosed by the fences.
Solution –
The total fences required were 100 of length 10 cm each. As the cricket stadium is circular, or we assume it to be circular, the fence makes the boundary of the stadium.
Thus, the total length of the boundary is – 10010=1000 cm=10 m.
Now, the space enclosed by the fence is a circle; thus, evaluating the area using the boundary, we get,
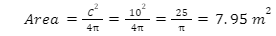
Thus, the area of the cricket stadium is 7.95 m2.
Application of the Area of a Circle
The area of the circle can be used infinitely in many sectors. This can be used in different bakeries to make pizza or cake with a definite radius and area covered on the pan. Also, the area covered by the football stadium or cricket stadium can be evaluated using the area of a circle. Different Ferris wheels or the wheel of cars can be used to find the area of the circle and the distance it covers all over.
Conclusion
The important points to remember in this concept are –
- The area of the circle can be computed if the radius or the circumference is known or given.
- The ratio is the mathematical constant for the diameter and the circumference of any circle.
- The sector in a circle is the area between any two circle radii. Moreover, the circumference consumed by the sector formed is the arc. The length of the arc can be different for each pair of radii.
- The circle is a point circle if it does not enclose an area, and the radius of such a circle is 0.
