Profile
Settings
Refer your friends
Sign out
The Perimeter of Rhombus Formula
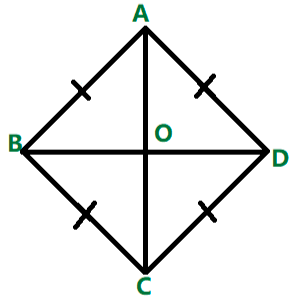
The rhombus is a two-dimensional figure. The rhombus is also known as equilateral quadrilateral as it has equal sides. Rhombus has opposite sides parallel and opposite sides are equal. Square and Rhombus have similar properties. All the sides of the rhombus and square are equal.
Perimeter is the total of its four sides or the sum of the length of boundaries. As all the sides of the Rhombus are the same, the length of one side is multiplied by 4.
Perimeter = 4(a)
“a” is the value of the side of the rhombus
Properties of Rhombus
Rhombus has 4 sides and all the sides are equal
Rhombus’s opposite sides are parallel
Rhombus’s opposite angles are equal
Diagonals cut each other at right angle
Total of any two adjacent angles is always 180 degree
Diagonal divides the vertex angles
When diagonals are given and perimeter is to be found out
Perimeter = 2 √d12+ d22
When the perimeter is to be found out with diagonals, the side of the rhombus is found using the Pythagoras theorem. With the help of these below properties.
Rhombus bisects into 4 congruent at right angle triangle in two diagonals
Diagonals divide each other at right angle
The formula to find the area of a rhombus is
A = ½ x d1 x d2
d1= Diagonal length d1
d2 = Diagonal length d2
Area of rhombus when base and height of rhombus is provided
Area = B ✕ H
B= Base of Rhombus
H= Height of Rhombus
Examples
1. Find the perimeter of the rhombus with diagonals 9 inches and 5 inches.
Perimeter = 2 √ d12+ d22
=2√92+52
=2√106
= 20.59 inches
Area of rhombus
A = ½ x d1 x d2
= ½ x 9 x 5
=22.5 inches
2. PQRS is a rhombus, one side is 6 units. Find the perimeter of PQRS.
As all sides of the rhombus are equal. A=6
Perimeter = 4(a)
=4(6)
= 24 units
3. ABCD is a rhombus. Its perimeter is 20. Find the side of the rhombus.
Given data, Perimeter=20
Perimeter = 4(a)
20 = 4 (a)
20/4 = a
a= 5
