Profile
Settings
Refer your friends
Sign out
Tan Theta Formula
Small Description: Tan Theta, including sine and cosine, is one of the 3 most prevalent trigonometric functions.
In a right-angle triangle, the tangent function is defined as the ratio or the quotient of the opposite side to that of the adjacent side.
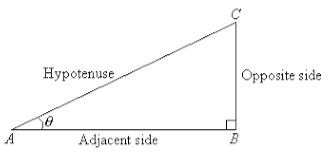
The mathematical denotation of the tangent is,
tan(θ)=Opposite Side/Adjacent Side
A table of tan theta values for various degrees and radians is provided below.
Radians | Degree | Tangent Value |
0 | 0 | 0 |
π/6 | 30 | 1/√3 |
π/4 | 45 | 1 |
π/3 | 60 | √3 |
π/6 | 90 | ∞ |
π | 180 | 0 |
3π/2 | 270 | ∞ |
2π | 360 | 0 |
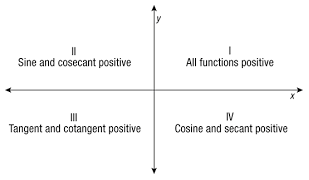
Reciprocal Identity Tangent Formulas
We already know that the tangent function and the cotangent function are reciprocals. In other words, if tan x = a / b, then cot x = b / a. As a result, the tangent formula employing one of the reciprocal identities is,
tan x = 1 / (cot x)
How to Find a Tangent?
To find the tangent, you must first find the hypotenuse. The hypotenuse is the longest side of a right triangle. The next step is to choose an angle. There are only two options for angles. You can’t pick the best angle. After you’ve decided on an angle, mark the sides. The opposite side will become the opposite side, and the adjacent side will be the side beside the angle.
Solved Examples
1. If sin (x) = 4/5, calculate the value of tan (x).
Using trigonometric identity, cos2(x)=1–sin2(x)=1–16/25
cos²(x)=9/25
cos(x)=3/5.
Now,tan(x)=sin(x)cos(x)=4/5 ✖ 3/5
∴ tan(x)=4/3
