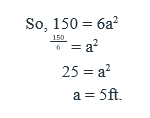Surface Area of a Cube Formula with Solved Example

Surface Area of a cube Formula with solved example

An object with six square faces, sides, or facets is called a cube, which has three lines meeting at each vertex in three dimensions. It is one of five Platonic solids and the only regular hexahedron. There are 6 faces, 12 edges, and 8 vertices. In addition to the cube, there is a cuboid in every dimension, as well as a right rhombohedron and a 3-zonohedron. It is a trapezohedron in four orientations, a square prism in three orientations, and a trapezohedron in trigonal form. A cube is dual to an octahedron. The symmetry of the object is cubic or octahedral. Among convex polyhedra, only the cube has all square faces.

A cube’s surface area is equal to the sum of the surfaces that cover it. For the surface area of a cube, the length of its sides multiplied by six equals the surface area. This is represented by 6a2, where a denotes the side length. In essence, it is a measure of the total surface area.

Formula of the surface area of cube = 6a2

Solved Examples

Ques. Find the surface area of a cube of a side length of 8 cm.

Ans. According to question, a side of the cube = 8 cm

        As we know, the formula of the surface area of a cube = 6a2

        And a = 8 cm

       Therefore, Surface Area = 6 (8)2

                                              = 6 x 64

                                              = 384 cm 2

Ques. The surface area of a cube is 150 feet square. What is the length of the cube?

Ans. According to the question, Surface  area of a cube = 150 ft 2

        As the formula of the surface area of a cube = 6a2