Square Formula with Solved Examples

Square Formula

In mathematics, three major formulas are used in solving sums with squares. These are the perimeter of a square, area of a square and the diagonal length of a square.

Introduction

A square is a simple regular quadrilateral with four sides that are all the same shape and size as well as the angles are also the same. The four corners of the square are all right-angle corners. A square is a specific example of a rectangular shape having a little difference that here in the square all sides are equal, unlike a rectangle.

In this part, we’ll go through square formulae, which are a series of formulas that may be used to calculate a square’s diagonal length, area as well as the perimeter. Here’s a rundown of them:

Perimeter Formula

In any polygon the perimeter is found by adding its all sides. And therefore, for that the formula used is,

Perimeter (P)=a+a+a+a

Perimeter (P)=4a

Where,

a = side length of the square

Area Formula

The territory encompassed by a square’s perimeter can be described as an area  of the square. As previously stated, a square is little more than a rectangle having all four sides of similar length. As a result, we write area as:

Area (A)=aa

Area (A)=a²

Again here, a = side length of the square

Diagonal Length Formula

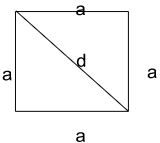
Speaking about diagonal, it is a line in a quadrilateral that connects two opposed sides. Simply, the  Pythagoras Theorem is used to calculate the diagonal length of a squared shape polygon as well as derive the formula for it.

The diagonal-line splits the square in 2 similar right-angled triangles in the diagram as shown below.  Because the neighboring sides of a square are similar in magnitude, the right-angled triangle is likewise an isosceles, having all of its isosceles sides measuring ‘a’ in span.

As a result, the Pythagoras theorem may be easily applied to these triangles shapes, with the perpendicular and base having ‘a’ units values and d as the unit value of the hypotenuse formed. As a result, we have:

d²=a²+a²

d=√2a²

d=a√2

Example

Let us understand the formula much better with the help of an example.

Consider a square field having the sides of it as 23 ft. A person has to build a swimming pool over there and has to find how much area will the pool cover. Along with the pavement length needed to be done on the boundary of the pool. He is also curious to know what could be the farthest straight line length to swim in the pool. Find out the details that the person wanted.

The side given in the question is 23 ft of the pool.

So, first the area of the pool will be found with the help of formula,

Area (A)=a²

A=232=529 ft²

Now, the pavement length is the perimeter,

Therefore formula for perimeter is,

Perimeter (P)=4a

P=423=92 ft

At last the maximum straight line distance that the person could swim in a square shaped pool is the diagonal length of the pool.

Therefore, the diagonal length of the pool can be found by using formula,

d=a√2

d=23√2=32.52 ft

Hence, the area covered by the swimming pool is 529 ft2, the measure of the pavement distance needed to be done on boundary is 92 ft as well as the maximum distance that the person could swim in a straight line in his pool is 32.52 ft.