Light travelling through air encounters various phenomena, including interference, refraction, reflection, and diffraction. Diffraction occurs when light encounters an obstacle.
The wavefront on the other side of a small opening is comparable in size to the wavelength λ of the light passing through it.
Observations of single slit diffraction can be made when light passes through a slit whose width (w) is on the order of the wavelength of the light. A distance L is greater than w from the slit determines the distance of the diffraction pattern on the screen. Diffraction intensity depends on the angle of incidence.
Body
- Let’s think about light coming from various parts of the same slit.
- They remain in phase when they travel straight ahead, and a central maximum is obtained. In spite of this, when rays travel at an angle θ with respect to an initial course, each travels an alternate distance to a typical location, and they may arrive in phase or not.
- Similarly, a ray from slightly above the middle will cancel out one from marginally above the bottom. A minimum in intensity occurs at this angle because each ray from the slit is destructively interfered with by another ray. In addition, there will be a minimum at the same angle and to one side of the incident direction of the light.
- Rays coming from the bottom travel a distance of one wavelength λ longer than those coming from the top. As a result, the ray from the middle travels a distance λ/2 further than the one from the left, arrives out of phase, and interferes destructively.
- The wavefront of the slit emits wavelets at all angles according to Huygens’ principle. Since the screen is extremely far away from the slit, rays heading in the right direction are nearly parallel.
- Light passing through a single slit is diffracted in all directions, and this interference may be helpful or destructive, depending on the angle. The path lengths of rays coming from the one or the other side of a slit are said to be determined by D sin θ.
- It can be observed that at the larger angle displayed, the path lengths vary by 3λ/2 for rays from the top and bottom of the slit. One ray is covering a distance λ unique in relation to the ray from the bottom and arriving in phase, interfering usefully. Two rays, each from somewhat above those two, will also add usefully.
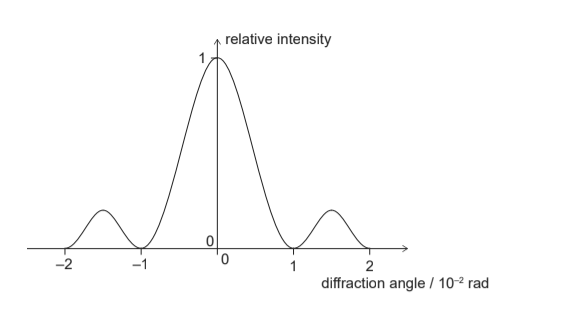
- Accordingly, to obtain destructive interference for a single slit, D sin θ = mλ, for m = 1,−1,2,−2,3, . . . (destructive), λ is the light’s wavelength, θ is the angle relative to the original bearing of the light, and m is the request for the minimum.where D is the slit width.
- Angular breadth of the central maximum of a single slit diffraction pattern is 60 degrees. Based on the central maximum’s intensity angle to the axis in a single-slit diffraction pattern, the central peak is 5.0 mm wide.There is an inverse relationship between slit width and the width of the diffraction maximum.The central maximum width is just the distance between the first order minima on either side of the screen from the centre. As the width size, ‘a’, is increased, the angle ‘T’ at which the intensity first approaches zero decreases, resulting in a narrower central band.
- The width of the central maxima is determined by the difference between the positions of the first two minima. Thus, we’ll apply the formula for minima position to get the formula for breadth of central maxima plus secondary maxima.
- Therefore, if monochromatic yellow light is switched with red light, the linear width will increase because red light has a longer wavelength than yellow light. In the same way, as the distance between the display and the slit increases, so does the linear width of the central maxima.
- Observations of the phenomenon of light bending or diffraction may be made using a single-slit diffraction. Additionally, due to this phenomenon, light from a coherent source interferes with itself, resulting in a distinctive pattern on the screen called the diffraction pattern.
- The central maxima, also known as the central fringe, is a characteristic feature of the diffraction pattern.The central maxima, also known as the central fringe, is a characteristic feature of the diffraction pattern. The central maxima is surrounded by dark and bright lines known as the secondary minima and maxima.
Conclusion
A field of study known as Diffraction has contributed to the development of precision spectrometers, which have significantly advanced Astronomy. At the beginning of the 1800s, two prestigious scientists fought for their lives in Italy and Germany, respectively. Diffraction is defined as the bending of light around a sharp corner of an obstacle. When light is reflected from a slit whose size corresponds to the wavelength of light, a pattern of dark and bright spots can be seen. This is known as single-slit diffraction.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






