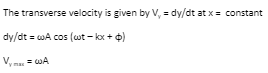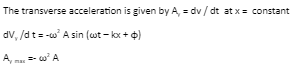Transverse

When the direction of propagation is perpendicular to the oscillation of constituents of the medium, it is known as a transverse wave. While propagating, these waves form alternate crests and troughs. 

We can use a string to illustrate these waves. When we pull a string in the vertical direction, we can conceive the development and propagation of the waves. The reason behind the formation of these waves is that the whole string is under tension. 

Here the stress is the little disturbance that we induce at one side of the string. This disruption propagates to its adjoining particles and continues, transferring the pulse along the length of the string. 

The particles oscillate at right angles to the propagation of the wave. The elements of the string oscillate about their mean position. Thus, a resulting disturbance is produced on the string which is called a sinusoidal wave.

Wave Motion

Disturbances occur when many constituents oscillate in a medium. The motion of such disruption is called a wave motion.

Types of Wave Motion

There are two types of wave motions:

• Longitudinal waves
• Transverse waves

Transverse Waves

The motion of mechanical waves involves oscillations of constituents of the medium. If the constituents of the medium oscillate perpendicular to the direction of wave propagation, it is called a transverse wave. Transverse waves travel in the form of crest and trough alternatively. 

Transverse waves cause a change in the shape elasticity but not in the density of the medium. 

Speed of Transverse Waves

Let us consider the waves in the string. Assume that:

• T is the tension that provides the restoring force in the string. It is the property of the stretched string arising due to an external force.
•  L is the linear mass density is an inertial property.
• M is the mass of the string.
• L is the length in which the string is divided.

The formula for the wave speed in the string is calculated by the dimensional analysis.

The formula for the wave speed in the string is calculated by the dimensional analysis.

The dimension of Mu is  [ML-1] and with tension T, it would be [MLT-2]. When we combine these dimensions, then we get the speed v which has dimension [LT-1].

Let us assume tension(T) and linear mass density () has the relevant physical quantities.

= C√ T/μ   ….(1)

In the above equation, C is the undetermined constant of dimensional analysis. Hence, C=1

The speed of transverse waves would be

ν= √T/μ

This speed of the transverse waves depends mainly on the properties of the medium tension T. It does not depend on the frequency or wavelength of the wave.

Longitudinal Waves

The mechanical waves oscillate between constituents of the medium. If they oscillate along the direction of wave propagation, it is called longitudinal waves. These waves propagate in the form of rarefaction and compression.

Longitudinal waves change the volume, elasticity, and pressure. They occur in all states of matter like solid, liquid, and gas. Like transverse waves, longitudinal waves undergo polarisation.

Speed of Longitudinal Waves

The constituents of the medium in longitudinal waves oscillate forward and backwards in the wave’s propagation direction. As we already know, longitudinal waves propagate in the form of rarefaction and compression.

Let B be the bulk modulus. The bulk modulus is the elastic property that determines the stress under the compressional strain.

The bulk modulus is given by:

K = ΔP / (ΔV / V)

where:

K: bulk modulus

ΔP: Variation in pressure or force acting on a material per unit area.

ΔV: change in material volume due to compression

V: Initial volume of material

The bulk modulus(B) and linear mass density () have the relevant physical quantities.

V =C√  B/ p

In the above equation, C is the undetermined constant of dimensional analysis. Hence, C=1

The speed of longitudinal waves would be

V =  √B/p

For a linear medium like a solid bar, the lateral expansion of the bar is negligible and is considered under longitudinal strain. The elastic modulus in Young’s modulus has the same dimension as the bulk modulus.

In a solid bar, the speed of longitudinal waves is given by

V = √Y/p

Where Y is Young’s modulus of the material of the bar.

This is well known that liquids and solids have higher speeds of sound than gases.  Because the gas has less compressibility property and higher value than the bulk modulus. It compensates for their higher densities than gases.

We can estimate the speed of sound in the ideal gas approximation.

For an ideal gas, volume V, temperature T, and pressure P are related by

P V = NK_BT

Where N is the number of molecules in volume (V).

K_B is the Boltzmann constant

T is the gas temperature

The isothermal change is expressed as

VΔP + PΔV = 0

Substitute B=P,

Then in an ideal gas, the speed of a longitudinal wave  is given by

V =  √P/p

This derivation was proposed by Newton and is known as Newton’s formula.

Examples of Longitudinal and Transverse Waves

Transverse Waves 

We can observe transverse waves in:

• Guitar string vibration
• Water ripples
• Electromagnetic waves
• Seismic waves

Longitudinal Waves 

There are many examples of longitudinal waves, such as:

• Seismic waves
• Sound waves
• Spring Vibration
• Tsunami waves

Conclusion

This article provides insights into the two types of wave motion- longitudinal and transverse waves. It also gives examples for both waves. This article explains the wave phenomenon in detail using a string as an illustration and derives the formulas for the speed of longitudinal and transverse waves.

Visualising Wave

Wave on the String is a type of mechanical wave. Usually, mechanical waves need a medium to travel, like sound waves. These waves originate from the disturbance in the medium and the disturbance propagated through the medium.

Types of mechanical waves

The mechanical waves are classified based on the medium’s physical properties, such as

• Number of dimensions
• The shape of wavefronts
• Periodicity
• The direction of particle motion

Speed, wavelength, frequency of the string wave

If the wave source makes vibrations with a constant time period, the wave frequency(f) will be equal to the source frequency.

When the source completes one vibration, the disturbance distributes out the surface and one wave will get generated. When the source keeps vibrating with constant frequency f, the wave is produced with constant frequency. This holds for all the wave motions.

The linear wave equation

We can describe the motion of any point on the string by using the wave function y = A sin (t – kx + ). The point on the string moves vertically and x remains constant.

Find the transverse Velocity(Vy)

Find the transverse acceleration (Ay)

This is the linear wave equation of the travelling mode, developed from a sinusoidal mechanical wave travelling the medium. It is also known as a differential equation, which describes the wave on the string.

The speed of a wave on a string is expressed as below

= T/

 T – tension (unit –  N)

is the mass per length of the string (in kg/m)

The speed of v and tension T are corresponding values at that point when the tension is nonuniform.

The principle of superposition

Consider two waves travelling at the same time along a similar extended string in inverse ways. We can see pictures of waveforms in the string at every moment of time. It is seen that the net relocation of any component of the string at a given time is the mathematical amount of the removals because of each wave.

The string is stretched too far, but the individual displacements are not added to give the resultant displacement. This takes place in nonlinear waves.

This principle is also expressed when overlapping waves are algebraically added to form a resultant wave. Overlapping waves do not alter the travel of each other. 

Amplitude of reflected and transmitted waves

Let v1 and v2 be the speeds of the incident wave and reflected wave in mediums, then

Power transmitted along the string by a sine wave

When a travelling wave is established on a string, energy is transmitted along the direction of propagation of the wave in the form of potential and kinetic energy.

Energy transferred in one time period = Pav t = energy stored in one wavelength.

Intensity

The intensity of the wave is given by the power transferred per second per unit cross-sectional area

Intensity = Power / Cross-sectional area

= P/s

Conclusion

In this article, We have seen the study material notes of visualising waves on the string. We have also gone through important concepts like the linear wave equation and power transmitted along the string by a sine wave. Along with this, there are many laws of transverse vibrations of a string in the sonometer wire.