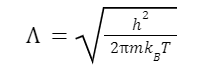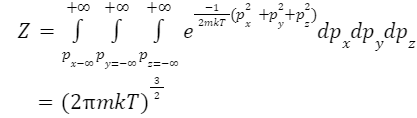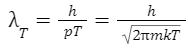Thermal De Broglie Wavelength

At the stated temperature, the thermal de Broglie wavelength is about the average De Broglie wavelength of the gas particles. It is defined as follows:

In this equation,

h represents the Planck constant, 

m represents the mass, 

k_B represents the Boltzmann constant,

and T represents the temperature. 

The thermal de Broglie wavelength is about the average De Broglie wavelength of gas particles in an ideal gas at the stated temperature.

The average interparticle spacing in the gas may be calculated as V/N^1/3, where V is the volume and N is the number of particles. When the thermal De Broglie wavelength is substantially shorter than the interparticle distance, the gas is classified as classical or Maxwell-Boltzmann. When the thermal De Broglie wavelength is equal to or greater than the interparticle distance, quantum processes take over and the gas must be classified as a Fermi gas or a Bose gas, depending on the nature of the gas particles. The critical temperature is the point at where these two regimes meet, and at this temperature, the thermal wavelength is nearly equal to the interparticle distance.

Thermal Wavelength

The thermal wavelength is an essential and useful statistic in thermodynamics because it quantifies the thermodynamic uncertainty in the localization of a particle of mass m with the average thermal momentum. It is commonly understood that for a 3-dimensional non-relativistic free ideal quantum system, the thermal wavelength can be used.

Photon: mass=0 kg, wavelength = 1.6483*10-5 m at 298 K is an example of the thermal De Broglie wavelength.

Importance of thermal De Broglie relationship

The gas will obey Maxwell-Boltzmann statistics when the interparticle distance is significantly greater than the thermal De Broglie wavelength. This is true for molecular or atomic gases at ambient temperature, as well as thermal neutrons emitted by a neutron source.

Equation of thermal De Broglie wavelength

The equation of thermal De Broglie wavelength is written as follows:

In the above equation, 

h is known as the Planck constant, 

m is the mass of the particle, 

k_B is known as the Boltzmann constant, 

T is the temperature.

Derivation of Thermal De Broglie wavelength

Consider an ideal gas whose partial function is given by

Therefore, the characteristic thermal momentum is given by 

pT = √(2mkT)

To derive the initial definition of the thermal de Broglie wavelength, consider the de Broglie wavelength of a particle with this characteristic momentum:

Thermal wavelength definition in general

Yan provided a comprehensive description of the thermal wavelength for an ideal quantum gas in any number of dimensions as well as a generalised connection between energy and momentum (dispersion relationship). It is useful in practice since there are various experimental circumstances with varying dimensionality and dispersion relationships.

If n  is the number of dimensions, and the relationship between energy (E) and momentum (p) is given by:

where a  and s  are constants, then the thermal wavelength is defined as:

when the Gamma function is used. For example, in the normal scenario of huge particles in a 3-D gas, we get n=3 and E=p²/2m, yielding the findings for massive particles given above. We have n=3 and E=pc for massless particles in a 3-D gas, which gives us the aforementioned findings for massless particles.

Conclusion

The thermal wavelength of particles in any positive dimension with any positive-exponent energy-momentum (i.e. dispersion) relation is discovered to be redefined. If a particle is significantly larger than its own de Broglie wavelength, or if it is interacting with other objects on a scale significantly larger than its de Broglie wavelength, then its wave-like properties are not noticeable. For everyday objects at normal speeds, λdB is far too small for us to see any observable quantum effects. A car of 1,000 kg travelling at 30 ms-1, has a de Broglie wavelength λdB = 2 × 10^-18 m, many orders of magnitude smaller than the sizes of atomic nuclei. A typical electron in a metal has a De Broglie wavelength is of order ~ 10 nm. Therefore, we see quantum-mechanical effects in the properties of a metal when the width of the sample is around that value. When the thermal De Broglie wavelength is substantially shorter than the interparticle distance, the gas is classified as classical or Maxwell-Boltzmann. When the thermal De Broglie wavelength is equal to or greater than the interparticle distance, quantum processes take over and the gas must be classified as a Fermi gas or a Bose gas, depending on the nature of the gas particles. The critical temperature is the point at where these two regimes meet, and at this temperature, the thermal wavelength is nearly equal to the interparticle distance. Thus, the thermal De Broglie relationship can be applicable for the ideal gas equation.