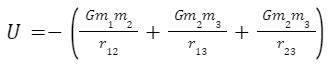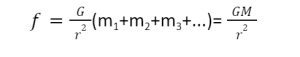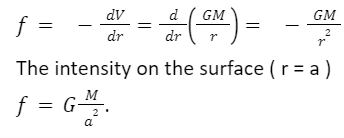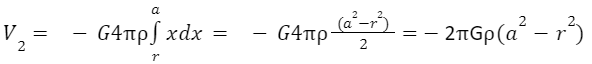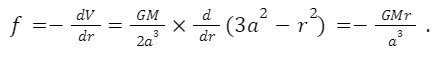The gravitational potential of a uniform solid sphere

According to Newton’s law of gravitation, every particle in this universe attracts another particle with force. The force is directly proportional to the product of their respective masses and inversely proportional to the square of the distance present in between them. This force is known as gravitational force.

Gravitational potential is the potential energy of a unit mass at that point because of the earth’s gravitational force. An energy that is possessed by an object due to its position in a gravitational field is called gravitational potential energy.

Gravitational Potential Energy

The gravitational potential energy U(r) of a system of two particles, with masses M and m and separated by a distance r, is the negative of the work that would be done by the gravitational force of either particle acting on the other if the separation between the particles were changed from infinite (very large) to r.  

Gravitational potential energy is given by- U=GMm/r. 

In a system of more than two particles, the total gravitational potential energy U is the sum of the terms representing all the pairs’ potential energies. For example, for three particles, of masses m1, m2, and m3,

Gravitational Potential Energy Formula

The equation for gravitational potential energy is:

Gravitational potential energy = mgh 

where,

• m represent the mass in kilograms
• acceleration due to gravity is g
• height above the ground level in metres is h.

Gravitational Potential of a Spherical Shell

Let us consider a thin uniform spherical shell of the radius (R) and mass (M) present in space. Now,

1. When point ‘P’ lies inside the spherical shell (r<R): 

As E = 0, V is a constant.

The gravitational potential is given by V = -GM/R.

2. When point ‘P’ lies on the surface of the spherical shell (r=R): 

On the surface of the earth, E = -GM/R².

Using the relation, V=-∫E.dr

with a limit of (0 to R), we will get,

Gravitational Potential (V) = -GM/R.

3: When point ‘P’ lies outside the spherical shell (r>R): 

Outside the spherical shell, E = -GM/r².

Using the relation, V=-∫E.dr

with a limit of (0 to r) we get,

V = -GM/r.

Gravitational Potential due to Uniform Solid Sphere

A solid sphere is supposed to be made up of many thin uniforms

concentric spherical shells, the masses of which are assumed to be

concentrated at the centre O. 

(i) At a point outside the sphere 

The potential due to such shells at an external point P is given as

where m1, m2, m3, etc. represent the masses of the shells which are under

consideration. Therefore,

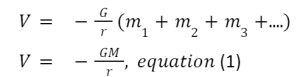
here M = m1 + m2+…, represents the mass of the solid sphere.

Here, intensity can be obtained by differentiating the expression for V when point P is outside the shell. Thus, differentiating Eq. (1), we get the intensity as:

(ii) The point P is on the sphere

The calculation is done exactly in a similar way, and it can be shown that the potential is given by

V= -GM/a

where a represents the radius of the solid sphere.

The intensity can be obtained by differentiating the expression for V when the point P is outside the surface of the shell. Thus, the intensity is given by

(iii) At a point inside the sphere

Let’s consider a point present inside the sphere such as P, which is at a distance of r from the centre O. The point P, is external to a solid sphere of radius r and internal to a thick shell of radii a and r. 

Let V1 and V2 denote the potentials at P due to these two parts. 

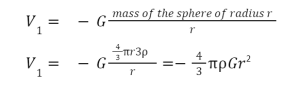
where is the density of the material of the sphere. 

To calculate V2, we consider a thin concentric spherical shell of radius x and thickness dx, of which P is an internal point. Therefore, as we have seen earlier, the potential at an internal point is equal to that on the surface; the potential at P due to the thin spherical shell under consideration is, given by-

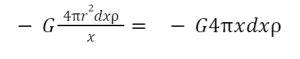
Hence, for the thick shell of radii a and r, the potential is given by

Hence, the potential at P due to the whole solid sphere is provided by

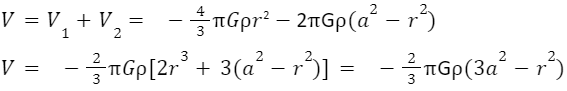
Now, the mass of the solid sphere is given by

Hence, the intensity at any internal point is given by:

Conclusion

The gravitational potential of a point in a gravitational field is the work done per unit mass that would have to be done by some externally applied force in order to bring a huge object to that point from some defined position of zero potential, usually infinity. 

The gravitational potential difference between the chosen point and the position has zero potential. While experiencing a gravitational force a particle moves from an initial point to a final point . The work done by that force and the change in gravitational potential energy is independent of the path taken.