Convex Lens
A typical optical lens is made up of two spherical surfaces. We call a lens a biconvex lens or simply a convex lens if those surfaces are curved outwards. The centre of these lenses is thicker, while the corners are thinner.
Furthermore, this type of lens can converge and concentrate a beam of light originating from the outside to a point on the other side. This point is referred to as the focus.
u versus v Graph
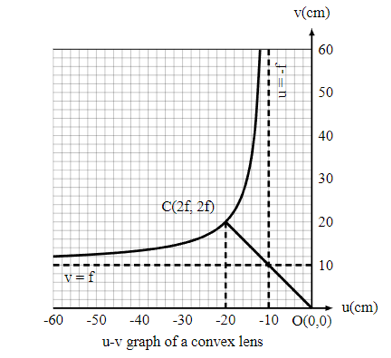
The graph depicts the u versus v graph. The following are the key points in the diagram:
- The graph is hyperbola, with asymptotes at u = -f and v = f, i.e., the image of an object placed at F is formed at infinity, and the image of an object placed at infinity is formed at F.
- The magnitudes of u and v are same at point C, but their signs are opposite, i.e., v = -u = 2f. This is the point where the u-v curve meets the straight line v = -u. When an object is put at a distance of 2f from the pole, its image is generated at the same distance (on the other side).
1/u versus 1/v Graph

The graph of 1/u versus 1/v is displayed in the figure. The graph shows a straight line with a slope of 1 and an intercept of 1f on the v-axis. When an object is put at infinity, 1/u equals zero. The image is created at the focus in this example, therefore v = f.
Concave Mirror
The reflecting surface of a concave mirror, also known as a converging mirror, is sunken inward (away from the incident light). Light is reflected inward by concave mirrors to a single focus point. They’re used to concentrate light. Concave mirrors, unlike convex mirrors, produce a variety of images based on the distance between the item and the mirror.
Converging mirrors collect light that falls on them, diverting parallel incoming rays into a focal. Because the normal to the mirror surface varies at different points on the mirror, light is reflected at varying angles at different spots.
u versus v Graph
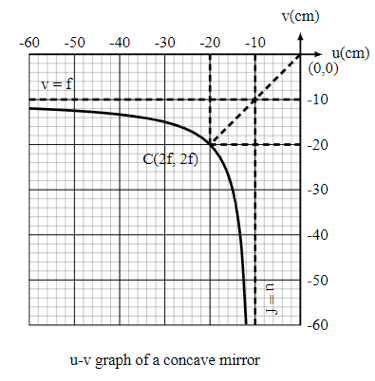
The graph depicts the u versus v graph. The following are the key points in this diagram:
- The graph is hyperbola with asymptotes at u = f and v = f, i.e., the image is created at infinity for the object put at F and at infinity for the object positioned at F.
- At point C, the values of u and v are equal, corresponding to u = v = 2f. This is the point where the u-v curve meets the straight line v = u. This represents the mirror’s curvature’s centre.
1/u versus 1/v Graph
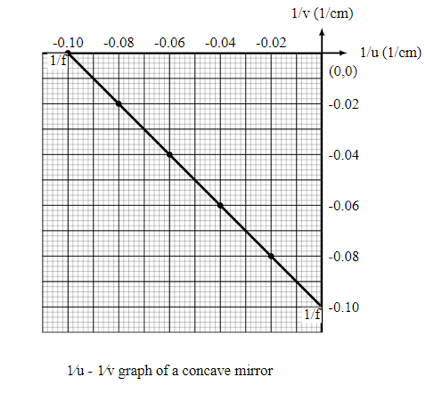
The graph of 1/u versus 1/v is displayed in the figure. The graph is a straight line with a slope of -1 and a 1/v-axis intercept of 1/f. When the object is put at infinity, 1/u equals zero. The image is created at the focus in this example, therefore v = f.
Finding focal length of concave mirror
The focal length of the concave mirror can be obtained in the following ways:
- A concave mirror is a spherical mirror with an inwardly curved reflecting surface that follows the laws of light reflection.
- Light rays from a faraway object can be thought of as being parallel to one another.
- The parallel rays of light meet the point in front of the mirror if the picture generated is actual, inverted, and very small in size.
- The image created by the convex lens is real and may be viewed on a monitor.
- The difference between the primary axis P and the focus F of the concave mirror is denoted by the letter f.
Finding the focal length of convex lens
The following are several methods for determining the focal length of a convex lens:
- The convex lens, also known as the converging lens, is thicker in the middle and thinner at the edges.
- On the other side of the convex lens, the refracted rays from the parallel beam of light converge.
- If the image is captured at the lens’s focus, it will be actual, reversed, and very small.
- The focal length of a lens is defined as the distance between the optical centre and the primary focus.
- As the image created by the lens is actual, it can be obtained on the screen.
Procedure of the u-v method Experiment
- Place the concave mirror on the stand that was provided. Arrange the screen on the table so that it displays the image of the distant item. Using a metre scale, measure the distance between the mirror and the screen. This distance is the mirror’s approximate focal length (f).
- Set the value of u to be between 1.5f and 2.5f. Divide the range into a set of steps that are all the same size.
- Position the mirror in front of a brightly lit object. Place the mirror at the distance u now (which is obtained as 1.5f).
- Place the screen on the table in front of the mirror, so that the reflected image is visible. Adjust the location of the screen to acquire a clear view of the thing while keeping the distance between the object and the mirror fixed. To acquire a precise image position, remove the parallax.
- Measure the distance between the mirror and the object, as well as the distance between the mirror and the screen. Assign these values to the letters u and v, accordingly. Using the formula f = uv/(u+v), find the focal length of the given concave mirror.
- Repeat the experiment with different values of u (up to 2.5f) and record v in the tabular column each time. Calculate the concave mirror’s focal length (f) each time.
- Calculate the mean of all focal lengths to determine the concave mirror’s correct focal length.
- Graphically, the focal length of the mirror may be determined by graphing graphs between u and v, as well as 1/u and 1/v.
Calibration of UV spectrophotometer
In the pharmaceutical industry, UV-Visible spectrophotometers are commonly utilised in the quality control department for analytical purposes. Calibration of the UV-Visible spectrophotometer is performed on a regular basis in order to preserve its accuracy and functioning conditions.
Calibration of UV-Visible spectrophotometer by parts
- Absorption cells
- Control of absorbance
- Photometric linearity
- Limit of stray light
- Resolution power
- Control of Wavelengths
Absorption cells
Fill the cuvette with milli-Q water at 240 nm, and the individual cuvette’s absorbance should not exceed 0.093.
One by one, rotate both cuvettes 180 degrees.
Acceptance criteria: The absorbance difference on rotation of the cuvette should be less than 0.005.
Control of absorbance
For UV region:
Prepared 0.005M sulfuric acid:
Weigh 60.0 mg of potassium dichromate that has been dried to a consistent weight at 130°C in 1000.0ml and dissolved in 0.005 M sulphuric acid with precision.
Using 0.005 M sulphuric acid as a blank, measure the absorbance at 235 nm, 257 nm, 313 nm, and 350 nm.
For visible region:
60.0 mg potassium dichromate, dried to constant weight at 130°C and transferred to a 100.0 ml volumetric flask, dissolved in 0.005 M sulphuric acid
Using 0.005M sulphuric acid as a blank, measure the absorbance at 430 nm.
Photometric Linearity:
In a 50 ml volumetric flask, dissolve 50 mg potassium dichromate in 0.005 M sulphuric acid.
Additionally, dilute the aforementioned solution as follows:
100 ml = 1 millilitre
100 ml x 2 millilitre
100 ml x 3 millilitre
100 ml x 4 millilitre
100 ml x 5 millilitre
At wavelengths of 235,257, 313 and 350 nm, take three consecutive readings of each dilution.
Acceptance criteria: With a mean value of 0.999 for each wavelength.
Limit of stray light
Using water as a blank, record the absorbance of a 1.2 percent potassium chloride solution in water at 200 nm.
Acceptance criteria: The absorbance should be at least 2.0.
Resolution power
At 250nm to 300nm, record the spectra of a 0.02 percent v/v toluene in hexane solution.
Acceptance criteria: The ratio of maximum absorbance at 269 nm to minimum absorbance at around 266 nm should not be less than 1.5.
Control of Wavelengths
To make a 4.0 percent w/v holmium oxide solution, dissolve 1.0 g of holmium oxide in.1.4M perchloric acid in 25 mL.
Using 1.4 M perchloric acid as a reference solution, record the spectrum of holmium perchlorate solution from 200 nm to 600 nm.
Wavelength | Maximum Tolerance |
241.14 | 240.15 to 242.15 |
287.15 | 286.15 to 288.15 |
361.50 | 360.50 to 362.50 |
536.30 | 533.30 to 539.30 |
Conclusion
A typical optical lens is made up of two spherical surfaces. We call a lens a biconvex lens or simply a convex lens if those surfaces are curved outwards. The centre of these lenses is thicker, while the corners are thinner. Furthermore, this type of lens can converge and concentrate a beam of light originating from the outside to a point on the other side. This point is referred to as the focus.
The reflecting surface of a concave mirror, also known as a converging mirror, is sunken inward (away from the incident light). Light is reflected inward by concave mirrors to a single focus point. They’re used to concentrate light. Concave mirrors, unlike convex mirrors, produce a variety of images based on the distance between the item and the mirror. Converging mirrors collect light that falls on them, diverting parallel incoming rays into a focal. Because the normal to the mirror surface varies at different points on the mirror, light is reflected at varying angles at different spots.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out



