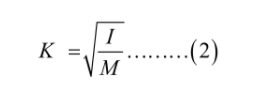The radius of gyration is always centred on a rotational axis. The radial distance from an axis at which a body’s mass is supposed to be concentrated and the moment of inertia equals the moment of inertia of the actual mass about the axis. The radius of gyration can be described mathematically as the root mean square distance of the specific point from the centre of gravity or the predefined axis, depending on the needed value.
The perpendicular distance is the distance determined from that point to the axis of rotation. The radius of gyration is well recognised for explaining the mass distribution of a spinning body about its axis of rotation. It is a measurement of a cross-sectional area’s elastic stability and stiffness in the face of a bulking force.
Radius of Gyration – Definition
In general, a radius of gyration is the distance from a body’s centre of mass at which the entire mass could be concentrated without affecting its moment of rotational inertia about an axis through the center of mass.
This is also known as the measure of how a rotating rigid body’s mass can be distributed along its axis of rotation.
Significance
- A more conservative estimate of the radius of gyration discloses the rotational axis at which the segment catches.
- It can also be used to adjust the intensity between cross-sections of a given section.
- In contrast to the presentation of many forms of fundamental shapes at the pressure hour, the range of gyration is helpful.
- When estimating the catching heap of a beam or pressure, the radius of gyration is important.
- With a lesser estimate of the radius of gyration, the primary investigation is successful.
Radius of gyration formula
The radius of gyration is defined as the root mean square distance between the object’s components and its center of mass or a specified axis. It is determined by the application. It is the angle formed by the perpendicular distance between the mass and the rotating axis.
The radius of gyration can be used to describe the trajectory of a moving point as a body. The regular distance covered by this point can be represented by the range of gyration at that place.
In terms of the radius of gyration, the formula for moment inertia is:
I = Mk2 …..(1)
The moment of inertia is represented by I, while the mass of the body is represented by m.
As a result, the gyration radius is as follows:
The moment of inertia of any rigid body may be calculated using the radius of gyration (1).
Consider a body made up of n particles, each has weight of m. Let us consider for the perpendicular distance from the pivot of rotation to particles. It is denoted by the letters r1, r2, r3,… rn. In terms of the radius of gyration, we can see that the condition produces the moment of inertia (1). We can calculate the body’s moment of inertia by substituting the qualities in the condition.
I = m1 r12+ m1r22+ m3 r32 + ……. + mn rn2……… (3)
If all particles have the same mass, equation (3) may be rewritten as
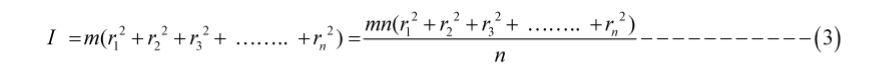
As a result, we may express mn as M, which denotes the body’s overall mass.
Therefore, the equation will be:
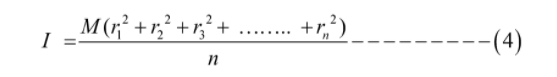
We may deduce the following from equation (4) and (1):
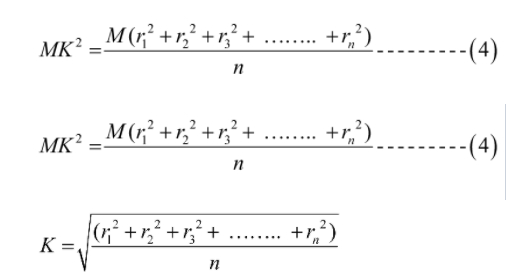
From final equation, we can say that the radius of gyration is the root-mean-square distance of various parts of the body. It is derived from the rotational axis.
Application of radius of Gyration
In Structural Engineering
The radius of gyration is defined as the dispersion of several segments of a specific item around a given body in material science and physics. It revolves around the central pivot, which is centred on the mass of the supplied body. This property helps in the assessment of a segment’s solidity in a precise way.
For given cross-sectional areas and segments with plane areas, the radius of gyration is used as an integral for calculating and determining the position of the clasp around the pivot. In engineering, this is done because the bodies are continuous chunks of matter that require an integral calculation.
In Molecular Physics
In polymer physics, the radius of gyration is used to calculate the dimensions of the polymer chain. The gyration radius is found to be related to the root mean square distance between the monomers. When it comes to molecular or polymer physics, the radius of gyration is calculated as an average across time.
The gyration radius is a significant property. Static light scattering, X-ray scattering, and small-angle neutron scattering are some of the additional experimental methods that can be used to determine it. The radius of gyration varies greatly depending on the object. To compute the radius of gyration of rods, cylinders, cones, rings, shells, and other objects, several formulae and data are used.
Conclusion
The radius of gyration is defined as the root mean square distance between the object’s components and its center of mass or a specified axis. The regular distance covered by this point can be represented by the range of gyration at that place. The radius of gyration is always centred on a rotational axis. The radius of gyration can be described mathematically as the root mean square distance of the specific point from the centre of gravity or the predefined axis, depending on the needed value. However there are various real life uses of the radius of gyration such as in molecular physics.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out