The symbol A-1 denotes the inverse of a matrix. It is only when the whole matrix is A. Many formulas are there that will help you calculate the matrix inverse. But before getting the inverse of a matrix, we must know about the points, i.e., adjacent and determinants. The matrix inverse is the type that will give completely different results from the first matrix. One finds the inverse of a matrix to get about the answers for the linear equations and many more. Here we provide you with the inverse of a matrix note that will help you know about the matrices.

What does the term inverse of a matrix stand for?

The matrix inverse can be calculated with different formulas. These different formulas will help you determine the inverse of a matrix. For getting the inverse of a matrix, there is the presence of prescribed formula. And while calculating the matrix inverse, you have to use that formula in a specified manner. 

• Firstly, we have to see the adjoint and determinant of the matrix. 
• Once we find these both, we have to move to the next step. We have to divide the adjoint of a matrix with its determinants.
• And lastly, we have to divide the adjoint by the determinants to get the inverse of a matrix.

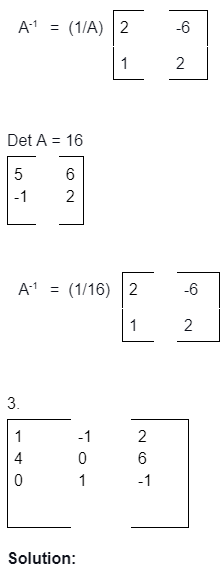
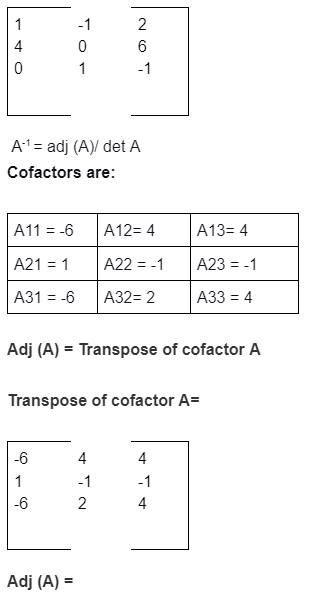
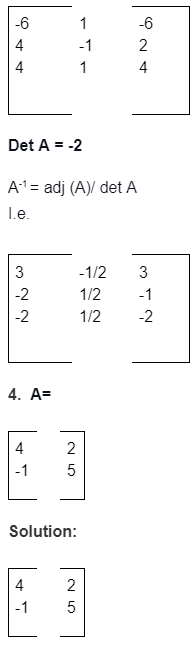
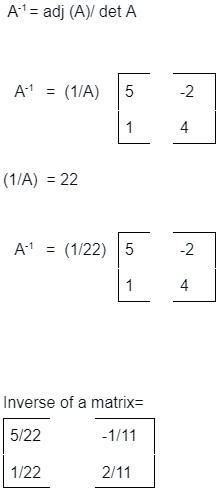
NOTE: The formula for the A matrix is adj (A)/ |A|; |A| is not equal to zero. We have to find the transpose of the matrix to solve the inverse of a matrix.

The inverse of matrix problems

Here the inverse of a matrix notes will discuss the inversion of a matrix using a specific formula. We provide you with the things that will help you know when you have to do the inverse of a matrix. Many simple things will help you determine these. Such main things are given below:

• When the determinant of a matrix is equal to zero, you can do the inverse of a matrix.
• Pay due consideration when the matrix is not equal to zero. In such a case, the matrix is degenerative or singular.

Examples: Here, we look at the inverse of matrix problems.