Parallel current carrying conductor

When a current is flowing through a wire, a magnetic field will be created around the wire to protect it. The magnetic field forms circular loops around the wire and the strength of these loops decreases as the distance between the wire and the observer increases. In order to determine the direction of the magnetic field, the right hand grip rule is applied:

• Wrap your index and middle fingers around the current-carrying conductor

• The thumb indicates the direction in which the current is flowing.
• The magnetic field is indicated by the direction of the fingers (often described as clockwise or anticlockwise depending on the view)

Two Current Carrying Conductors

In the case of two wires carrying current that are placed parallel to each other, the magnetic fields of the wires will interact, resulting in a force that acts between the wires and the conductor. The magnitude of the force acting on each wire is the same, but the directions in which it acts are diametrically opposed. This holds true even if the currents carried by the conductors are of varying magnitude.

The diagram below illustrates two examples in which the direction of the magnetic field around each wire is depicted with the “ • x “notation to indicate the direction of the magnetic field. Diagram A depicts the current flowing through the wires in the same direction, while diagram B depicts the current flowing through the wires in the opposite direction:

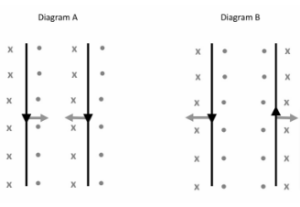
Determining the direction of the force

Looking at the direction of the individual fields in the area between the conductors, we can determine which way the force is moving:

• Using Diagram A, the fields are in opposition to one another, resulting in an attractive force.

• Similarly, in Diagram B, the fields are the same, resulting in a repellent force.

The rule of thumb is that whenever two conductors have current flowing in the same direction, the force will be attractive and whenever the currents are in the opposite direction of each other, the force will be repulsive.

Determining the magnitude of the force between two parallel conductors

The magnitude of the force acting between two parallel current carrying conductors is influenced by a number of factors, the most significant of which are:

• The current flowing through each conductor.

• The length of the conductors is measured in metres.

• The distance between the conductors is measured in metres.

The magnitude of the force acting between two parallel current carrying conductors can be calculated by using the following formula:…

Where:

F/l is the force per unit length between the conductors (in Nm−1)

µ0 is the magnetic permeability of free space (4π × 10−7 NA−2)*

I1 is the current in wire 1 (in A)

I2 is the current in wire 2 (in A)

r is the distance separating the conductors (in m)

It is possible to calculate the force between two long straight and parallel conductors that are separated by a distance r using the concepts that we have developed in the preceding sections. Figure 1 depicts the wires, their currents, the fields they generate and the forces they exert on one another as a result of their interactions. Consider the field produced by wire 1 and the force that it exerts on wire 2 in the diagram (call the force F2). According to the formula, the field due to I1 at a distance r is

Definition of ampere

l is the length of a segment of parallel wires carrying currents, and the force between them is,

As a result, the force per unit length of the conductor is equal to

Ampere is defined as follows in accordance with the conditions stated above.

When a constant current is flowing through two parallel infinitely long straight conductors of negligible cross section that are placed one metre apart in air or vacuum, the current experiences a force of 2 x 10-7 Newton per unit length of the conductor, which is known as an ampere.

Biot Savart law

The magnetic field produced at a point in space that is a certain distance away from a current carrying conductor is defined by the Biot-Savart law in magnetism and the magnetic field produced by the current flowing through the conductor is known as the induced magnetic field.

In accordance with Biot-law, Savart’s “the magnetic field due to a current-carrying conductor at a distance point is inversely proportional to square of distance between the conductor and the point and the magnetic field is directly proportional to the length of the conductor, current flowing through the conductor.” This is known as biot-Savart law.

Mathematically,

Where, B = magnetic field intensity

                 μ = permeability of free space

 N = number of turns

I = current intensity

R = radius

Conclusion

Because of their separation by a distance r, the force between two parallel currents I1 and I2 has a magnitude per unit length that is given by,

If the currents are flowing in the same direction, the force is attractive; if they are flowing in opposite directions, the force is repulsive.

An ampere is a unit of electric current equal to one Coulomb per second of flow