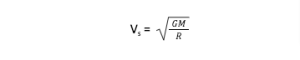Orbital Velocity of a Satellite

In this article, we discuss the concept of the orbital velocity of a satellite. It basically refers to the amount of velocity required by a satellite to be launched into the orbit of a planetary system. We further discuss the formula by which you can calculate the velocity required by a satellite to be launched into the orbit of a planet for it to stay in the given orbit.

We have also cleared the concept of the orbital speed of a satellite. In simple terms, the speed required by a satellite to orbit around a planetary system without losing its momentum is known as orbital speed. 

For better understanding, we have also discussed the formula to calculate the orbit speed of a satellite.

The orbital velocity of a satellite is the velocity required by the satellite to balance the gravitational pull and the inertia of the satellite’s motion. This concept can be further explained with the following example:

● Take, for instance, that we use a device to launch a certain object horizontally across the earth’s surface.

● At some point in time, the object would orbit across the earth’s surface for a certain distance and eventually fall on the earth’s surface.

● If we consider using a device that can create a velocity or speed of the exact amount that can launch the object into the earth’s orbit, the object would get stuck in the earth’s orbit and would not return to the surface.

● This velocity is known as the orbital velocity. This same concept is used in space physics to launch satellites into the earth’s surface.

Hence, this velocity required for a satellite to find a balance between the gravitational pull of the earth and the inertia of its motion is known as the orbital velocity of a satellite.

Orbital velocity equation

Orbital velocity can be defined as the velocity at which a body orbits around a celestial body or planet with a constant gravitational pull. Due to its orbital velocity, the satellite experiences a centrifugal force that cancels the gravitational pull and keeps moving in the orbit. 

The time taken by it for one revolution around the earth is known as its time period. The velocity required for an object to revolve around a planet in a circular orbit is called orbital velocity. It is denoted by Vo.

You can refer to the following equation for calculating the orbital velocity of a satellite.

The equation for orbital velocity is expressed as follows:

Vorbit = √GM/R

Where,

G denotes the gravitational constant

M denotes the mass of the body at the center

And, R denotes the radius of the orbit

Orbital speed equation

Orbital speed can be defined as the speed at which a celestial body, mainly a satellite, revolves around the orbit of another celestial body. The satellite revolves around a celestial body always greater in mass than the satellite.

Just as the earth orbits around the sun, the moon orbits around the earth. The earth’s orbital speed around the sun is 108,000 km per hour. The orbital speed of a satellite is influenced by its vertical distance or altitude from the earth’s surface.

Now, since a satellite always stays right at the same position in the earth’s orbit, it is commonly known as “geostationary orbit.” These satellites are mainly used for cartography and climatology.

This simply means that the higher the satellite is in the earth’s orbit, the less likely it is to move or shift its position; this is mainly because the higher orbits of the earth are closer to outer space, which is essentially a vacuum.

Hence, the satellites in the higher orbits of the earth experience the least amount of drag force or aerial drag and therefore can stay in the earth’s orbit in the same spot for centuries, such as the moon.

The equation for orbital speed can be expressed as follows:

 Vorbit =2πa/T 

Where,

Vc  denotes the orbital velocity

a denotes the length of the semi-major axis in meters

and T denotes the orbital period

 Speed of satellite formula

The formula for centripetal force and gravitation is used to derive the equation for calculating the speed for the orbital velocity of a satellite.

To circle an orbit of the earth almost 35,786 km far from the earth’s surface, the satellite would have to maintain a velocity of about 11,300 km/h. This orbital speed and distance allow the satellite to revolve around the earth in 24 hours.

The following expression can calculate the speed of a satellite:

Vorbit = √GM/R

Where,

G denotes the gravitational constant

M denotes the mass of the body at the center

And, R denotes the radius of the orbit

Conclusion

The orbital velocity is the speed required by a satellite to maintain a balance between the gravitational pull of the celestial body or planet it is orbiting and the inertia of its motion.

In simple terms, orbital velocity can be defined as the speed or velocity required by a satellite to keep orbiting a celestial body without losing velocity. Also, the satellite revolves around a celestial body that is always greater in mass than the satellite