Profile
Settings
Refer your friends
Sign out
We all know that when the values are very small, they are difficult to solve. At such times integration comes into the picture. It is the method to unit the small parts or values to find out the value of the whole. In physics, it is normally used to find out the areas of the bounded regions. This is done by finding the function with the given differential. So, let us learn more about integration in this article and get an overview of integration methods and some of the integration rules.
Definition of integration
Finding functions whose derivative is given is known as anti-differentiation or integration. When we cannot perform general addition operations, we use integration to feature values on an outsized scale.
Rules for Integration:
- A constant is always included in the expression for the indefinite integral, i.e.,
If g′(x)=f(x), then∫f(x)dx=g(x)+Cifg′(x)=f(x), then∫f(x)dx=g(x)+C, since, the derivative of a constant is 0.
- The integral of a derivative gives back the same function itself (with a constant):
∫f′(x)dx=f(x)+C∫f′(x)dx=f(x)+C
If we do the derivation of an equation we get the same function:
ddx(∫f(x)dx)=f(x)
- 3. ∫{f(x)±g(x)}dx=∫f(x)dx+∫g(x)dx∫{f(x)±g(x)}dx=∫f(x)dx+∫g(x)dx
- 4. ∫kf(x)dx=k∫f(x)dx∫kf(x)dx=k∫f(x)dx
- ∫f(x)dx=g(x)+C, ∫f(x)dx=g(x)+C, then
∫f(ax+b)dx= 1/a*g(ax+b)+C
Methods of Integration
Substitution Method
Integration can be solved by introducing a new independent variable when it is difficult to seek out the integration of a function. By changing the independent variable x to t, in a given form of integral function, say (∫f(x)). (∫f(x)), we can transform the integral.
Let’s substitute the value of independent x = g(t) in the integral function ∫f(x),
We get, dx / dt = g’(t)
Or, dx = g’(t) • dt
Thus, from the above substitution, we get,
I=∫f(x).dx=f(g(t).g′(t)).dt
I=∫f(x).dx=f(g(t).g′(t)).dt
Parts Integration method
This Integration rule is employed to seek out the integral of two functions.
By product rule of derivatives, we have
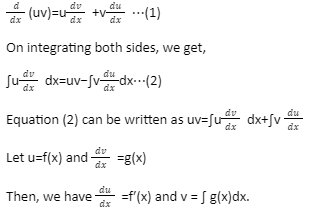
So, Equation (2) becomes
∫f(x)g(x)dx=f(x)∫g(x)dx−∫[f′(x)∫g(x)dx]dx
Using Trigonometric Identities –
To simplify any integral function that consists of trigonometric functions, trigonometric identities are used.
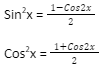
Particular Functions Integration
Integration of various particular functions have some important formulae of integration that will be applied to form other integration into the quality sort of integrand. Integration of those standard integrands are often easily found employing a direct sort of integration methods. Here are the 6 important formulas listed below –
- ∫ dx/ (x²– a²) = ½ a log | (x – a) / (x + a) | + c
- ∫ dx /√ (a² – x²) = sin–¹ (xa) + c
- ∫ dx /√ (x² + a²) = log | x + √(x² + a²) | + c
- ∫ dx/ (a² – x²) = ½ a log | (a + x) / (a – x) | + c
- ∫ dx /√ (x² – a²) = log| x+√(x² – a²) | + c
- ∫ dx / (x² + a²) = 1/a tan–1 (x/a) + c
Where, c = constant
Using Partial Factors
Let us find out the value of A and B
We get, 1=A(x+2)+B(x+1), when we compare the equation.
From this, we get a group of two linear equations.
A+B=0 and 2A+B =1
If we solve the equation we get, A=1 and B=-1.
Integration methods examples
Calculate ∫ cos2 x dx
Integrate the function f(x)=2x sin(x2+1) with respect to x.
Solution:
Let x2+1=z
Then, 2x dx = dz
∫f(x)dx=∫2xsin(x2+1)dx
=∫sinz dz=−cosz+C
=−cos(x2+1)+C
∴∫2xsin(x2+1)dx = −cos(x2+1) + C
Conclusion
Thus, to conclude, there are 5 integration methods-
The substitution method is when integration can be solved by introducing a new independent variable when it is difficult to seek out the integration of a function. Parts integration method is employed to seek out the integral of two functions. Using trigonometric identities to simplify an integral function that consists of trigonometric functions.
Partial Fraction, Particular Integration functions have some important formulae of integration which will be applied to form other integration into the integrand in standard form.
By using integration by substitution.
