A magnetic field can be produced by moving charges or electric currents. The basic equation governing the magnetic field due to a current distribution is the Biot-Savart law. Solenoid is a coil which has length and is used to produce a uniform magnetic field . Magnetism is an attractive or repulsive ability produced by moving electric charge.

Motion of  charge in uniform magnetic field

When a charge +q is projected in uniform transverse magnetic field (θ=90°,v⟂B), then maximum magnetic force of constant magnitude always acts perpendicular to its direction of motion so the charge moves along circular path and required centripetal force provided by the magnetic force.

Radius of circular path

    r=mv/qB =p/qB =√2mE/qB =√2mqv/qB

r ∝ v ∝ p ∝ √E ∝ √v

Magnetic effect of current

Magnetic field is established by moving electric charges(current) and in turn the field can exert a force (magnetic) on the other moving electric charges(current element).

Biot-Savart Law:

   Magnetic field at a point p due to a current element Idl depends as

                                          dB ∝I ; dB ∝ dl; dB ∝ sinθ

                                             B ∝ 1/r2

On combining , dB ∝ Idl sinθ/r2

                dB=k Idl sinθ/r2

                 Where k=𝜇0/4𝜫

Magnetic force on a moving charge 

         F=q(v✕B)

Magnetic field lines

• Magnetic field lines are closed curves.
• Tangent drawn at any point on the field line represents the direction of the field at that point.
• Field lines never intersect with each other.
• At any place crowded lines represent stronger fields while distant lines represent weaker fields.
• In any region, if field lines are equidistant and straight the field is uniform otherwise not.
• Magnetic field lines can be mapped by using iron dust or using a small magnetic needle.

Magnetic field due to current carrying straight conductor or wire

• Finite length wire: Magnetic field due to finite length wire at point P

               B=𝜇0 I (sinθ1+sinθ2)/4𝜫d

• Infinite length wire : magnetic field due to infinite length wire at point p

           B=𝜇0 I (sin90°+sin90°)/4𝜫d

• Semi infinite length wire : Magnetic field due to semi infinite length wire at point p

          B=𝜇0 I (sinθ+1)/4𝜫d

• Magnetic field at the centre of current carrying circular loop and coil

  B=𝜇0 N I /2R

 Where N = number of turns in coil

Magnetic field at axial point of the current carrying circular coil

        B=𝜇0 N I R2/2(x2+R2)(3/2)

Magnetic Flux

The number of magnetic field lines which are crossing through a given area of cross section is called magnetic flux of the area.

Magnetic flux through a coil of N turns and A area of cross section ɸ=N(B.A)=NBA cos θ

Ampere’s circuital law

It states that line integral of the magnetic field along any closed path in free space is equal to 𝜇0 times of net current , which passes through an area bounded by the closed path.

Mathematically, ∮B.dl=𝜇0 ∑ I

The solenoid

• It is a coil which has length and is used to produce a uniform magnetic field of long range.
• Magnetic field on the axial point inside of solenoid of finite length

        B=𝜇0nI(cosθ1-cosθ2)/2 

• If solenoid length is infinite then

    B=𝜇0nI

• Magnetic field at end point of infinite solenoid

       B=𝜇0nI/2

• Magnetic field outside the volume of the infinite solenoid approaches zero. If magnetic permeability of solenoid frame is 𝝁r then field produced by the solenoid B=𝜇0 𝝁r nI

Toroid 

A toroid can be considered as a ring shaped closed solenoid. 

Magnetic field inside a toroid by Ampere’s Circuital Law is given as B=𝜇0nI

     Where n= turn density = N/2𝜫R

 N= total number of turns 

 R= mean radius of toroid=(R1+R2)/2

R1 and R2 are internal and external radii of toroid respectively.

Magnetic Dipole

Magnetic moment of current carrying coil (or loop)

•   Current carrying coil(or loop) behaves like a magnetic dipole . The face of the coil in which current appears to flow ACW acts as the north pole while the face of the coil in which current appears to flow CW acts as the south pole .
• A loop of geometrical area A, carries a current I then its magnetic moment is given as M=IA
• For a coil of turns N, M=NIA

Torque on magnetic dipole

ꞇ=M✕B

Work done in rotating a magnetic dipole in a uniform magnetic field W=MB(cosθ1-cosθ2)

Potential energy of a magnetic dipole is the work done in rotating the dipole through an angle θ with respect to a direction perpendicular to the field .

U=-MBcosθ=-M.B

Moving coil galvanometer

It is an instrument used for the detection of small current .

Principle : When a current carrying coil is placed in a magnetic field , it experiences a torque. 

In a moving coil galvanometer the current I passing through the galvanometer is directly proportional to its deflection(θ ).

I ∝ θ , I=Gθ.

Where G=k/NAB

 G – galvanometer constant

A- area of a coil ,N- number of turns in the coil,

B= strength of magnetic field ,k= torsional constant of the spring i.e. restoring torque per unit twist.

Magnetism

Vibration magnetometer

It is an instrument used to determine the magnetic moment of a magnet ,to compare the horizontal component of earth’s magnetic field at two different places and the magnetic θmoment of two bar magnets.

Principle : Whenever a freely suspended bar magnet in earth’s horizontal magnetic field BH is slightly disturbed from its equilibrium position then it will experience a torque and execute angular S.H.M,

Time period of angular S.H.M .

T=2𝜫/w=2𝜫√(I/MB)

 I= moment of inertia of bar magnet 

M= magnetic moment of bar magnet

The Earth’s magnetism

• It is hypothesised that circulating ions in the highly conducting liquid region of the earth’s core could form current loops and produce a magnetic field .

Elements of the earth’s magnetic field.

•  Magnetic declination : Magnetic declination at a place is defined as the angle between the geographic meridian and magnetic meridian .
• Magnetic dip or inclination : Magnetic dip at a place is defined as the angle made by the earth’s magnetic field with the horizontal in the magnetic meridian .
• Horizontal component of earth’s magnetic field (BH) 

At a given place the horizontal component of earth’s magnetic field is the component of the resultant magnetic field of the earth along the horizontal line in the magnetic meridian .

Horizontal component  BH =Bcosθ

Vertical component     BV =Bsinθ

      Tanθ = BV/BH

Magnetisation and magnetic intensity

Net magnetic moment per unit volume of a sample known as its magnetisation (M).

  M = mnet /V ,

For current in coils and conductors , magnetic intensity H is defined as 

  H = B0/ 𝝁0 =nI

When a magnetic field is applied to material , the material gets magnetised. The actual magnetic field (B) inside the material is the sum of the applied magnetic field (B0) and the magnetic field due to magnetisation (M).

  B =B0 +𝝁0M

  B = 𝝁0(H+M)

Classification of magnetic materials

On the basis of magnetic properties of the material those are divided in three classes.

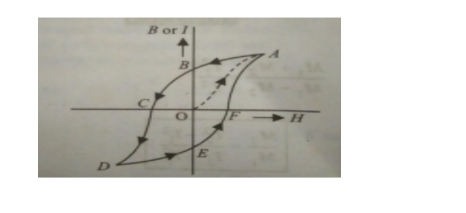
 Hysteresis 

•  The phenomenon of lagging of the magnetic induction behind the magnetising field in a ferromagnetic material is called hysteresis .The area of the hysteresis (B-H) loop gives the energy wasted in a sample when it is taken through a cycle of magnetisation .
• The magnetic induction left behind in the sample after the removal of the magnetising field is called retentivity.
• The value of the reverse magnetising field required to make the residual magnetism of a sample equal to zero is called coercivity.