Lorentz transformation is the relationship between two different coordinate frames that are moving at a constant velocity and are relative to one another in space and time, respectively. Hendrik Lorentz, a Dutch physicist, is credited with giving the transformation its name.
There are two frames of reference, and they are as follows
- A constant velocity is maintained throughout the motion of an inertial frame.
- Non-Inertial Frames – Rotational motion with constant angular velocity and acceleration in curved paths with constant angular velocity and acceleration
Lorentz transformation is only relevant to changes in inertial frames, and it is usually discussed in the context of special relativity. In this type of linear transformation, mapping occurs between two modules that both contain vector spaces, and the result is a linear transformation. Scalar multiplication and addition are preserved in linear transformation, as are the operations of multiplication and addition. Several intuitive characteristics of this transformation exist, such as the fact that an observer moving at different speeds can measure elapsed times, different distances, and the ordering of events, but the condition that must be met is that the speed of light must be the same in all of the inertial frames.
It is also possible for Lorentz transformation to include rotation of space; a rotation that is not affected by this transformation is known as a Lorentz Boost. When this transformation is applied to any two events, the space-time interval that occurs between them is preserved.
Formula for the Lorentz Transformation
The following is the mathematical representation of the Lorentz transformation:
t’=𝜸[t – (vx/c2)]
x’=𝜸[x-vt]
y’=y
z’=z
Where,
A point on the coordinates of an event in two frames is represented by the coordinates (t,x,y,z) and (t’,x’,y’,z’).
v is the velocity that is restricted to the x-axis.
The speed of light is represented by the symbol c.
Eqns of the Lorentz Transformation (Lorentz Transformation Equations)
These are the coordinates defined in the stationary reference frame F: x, y, z, and time (in milliseconds). There is another reference frame F’ that is moving at a velocity v that is relative to the first reference frame F, and the observer defines the coordinates of this moving reference frame as x’, y’,z’, and t’ in this moving reference frame. The coordinate axes are parallel in both reference frames, and they remain perpendicular to one another at all times. The relative motion is in the direction of the xx’ axes.
At t = t’ = 0, the origins in both reference frames are same (x,y,z) = (x’,y’,z’) = (0,0,0)
If the events x, y, z, and t are recorded in reference frames F, then the coordinates of these events have the following value in reference frames F’:
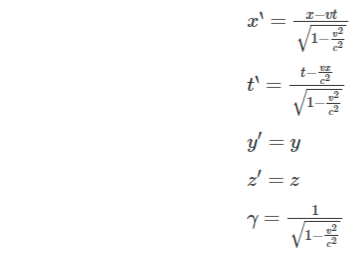
The Lorentz factor is denoted by the lowercase gamma.
The following is the result of the above equation, which is known as the Lorentz transformation:
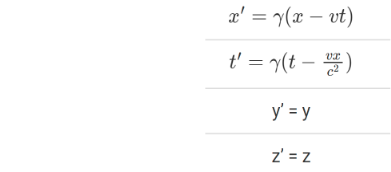
Lorentz Transformation in Inertial Frame
A Lorentz transformation can only be used in the context of inertial frames, which is why it is commonly referred to as a special relativity transformation when applied to ordinary objects. During the linear transformation, a mapping is created between two modules that both contain vector spaces as components. With the use of a linear transformation, the results of multiplication and addition operations on scalars are preserved. It is important to remember that the speed of light should be the same across all frames of reference as a result of this transformation; otherwise, the observer moving at different speeds will be able to measure different elapsed times, different distances, and different events in the correct order.
The Statement of the Principle
Known as transformation equations, Hendrik Lorentz’s transformation equations are used to relate two different coordinate systems in an inertial reference frame. Lorentz transformations are made possible by two laws of physics:
- Relativity Principle
- Light’s constant speed
Space-Time
To comprehend the concept of Lorentz transformation, we must first comprehend the nature of spacetime and the coordinate system that exists within it.
Space-time coordinates, as opposed to three-dimensional coordinate systems with x, y, and z axes, specify both space and time in one coordinate system (four-dimensional coordinate system). In four-dimensional spacetime, the coordinates of each point are made up of three spatial characteristics and one temporal characteristic.
The Importance of a Space-Time Coordinating System
Previously, time was considered to be an absolute quantity. In light of the fact that space is not an absolute quantity, observers would disagree about the distance travelled (and, consequently, they would disagree about the speed of light), even though they would agree on the amount of time it takes for the light to travel the distance.
As a result of the Theory of Relativity, time is no longer considered to be an absolute quantity.
As a result, it is now possible to calculate the distance between two events as a function of time.
d = (1/2)c
Where,
d-distance between the event and the observer
The time it took for a pulse to travel to the event and return was measured in t.
light travels at the speed of c
When it comes to space and time as separate and independent components, the theory of relativity has fundamentally altered our perceptions of them. As a result, space and time had to be combined into a single continuous entity.
Conclusion
Lorentz transformation is only relevant to changes in inertial frames, and it is usually discussed in the context of special relativity. In this type of linear transformation, mapping occurs between two modules that both contain vector spaces, and the result is a linear transformation. Scalar multiplication and addition are preserved in linear transformation, as are the operations of multiplication and addition. Several intuitive characteristics of this transformation exist, such as the fact that an observer moving at different speeds can measure elapsed times, different distances, and the ordering of events, but the condition that must be met is that the speed of light must be the same in all of the inertial frames.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






