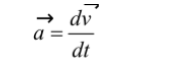Kinematics

Kinematics is the science that describes the movement of objects using words, diagrams, numbers, graphs, and equations. Kinematics is a part of mechanics. The goal of any study of kinematics is to result in sophisticated mental models which can be used to describe (or explain) the motion of real objects.

Kinematics is beneficial in conceptual design of mechanical systems. At the starting geometries and velocities of objects are components of the model. Kinematics help to decide whether or not a design is theoretically possible, there are more complexities while designing something for the world.

Important terminologies

Vector

A vector is a physical quantity that has both direction as well as magnitude, like velocity or force. In contrast, a quantity which has only magnitude but not direction, like temperature or time, is known as a scalar. A vector is usually denoted by an arrow whose length is proportional to the magnitude of physical quantity and whose direction is indicated by the orientation of the arrowhead.

Displacement

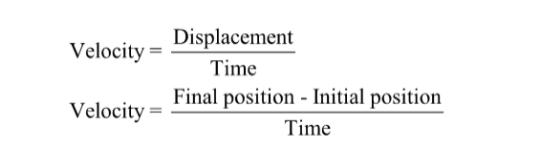
The displacement is the change in the position of an object with respect to the reference frame. For example, when a car is moving from a house to a grocery store, then its displacement is the relative distance from the grocery store to the frame of reference or the house.

Displacement is given as

Here,

Δx= displacement

x_f= final position

x_i= initial position

Velocity

Velocity is a Physical Vector Quantity. Velocity has both magnitude and direction also. In calculus, velocity is defined as the first derivative of the position with respect to time period. Velocity is also defined as the rate of change in the position of an object w.r.t time.

SI unit of velocity is meter per second which is given as m/s.

Average Velocity

Average velocity is defined as the total displacement travelled by a body in a given interval of time.

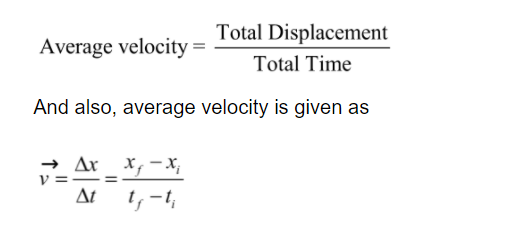
Here,

t_f= final time

t_i= initial time

Acceleration

Acceleration is defined as the rate of change of velocity w.r.t time. Acceleration is given as

Kinematics Equation

The kinematics equation includes five variables of kinematics which are

1. Displacement.
2. Initial velocity.
3. Final velocity.
4. Time interval.
5. Constant acceleration.

In essence, the kinematic equations can derive one or more of these variables when others are given already. These equations define constant velocity or constant acceleration motion. Since the kinematic equations only apply to constant acceleration or constant velocity, we cannot use them. when either of them changes.

The basic kinematics equations are

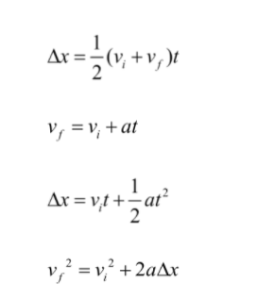
Kinematics in One Dimensions

In one-dimensional kinematics we assume a particle which is moving along a straight line. For the special case of constant acceleration, we can derive equations of motion. When deriving these equations of motion, we assume that the particle only moves in a straight line along the x-axis.

We know that, the total displacement is given as

Integrate the equation of velocity then we get

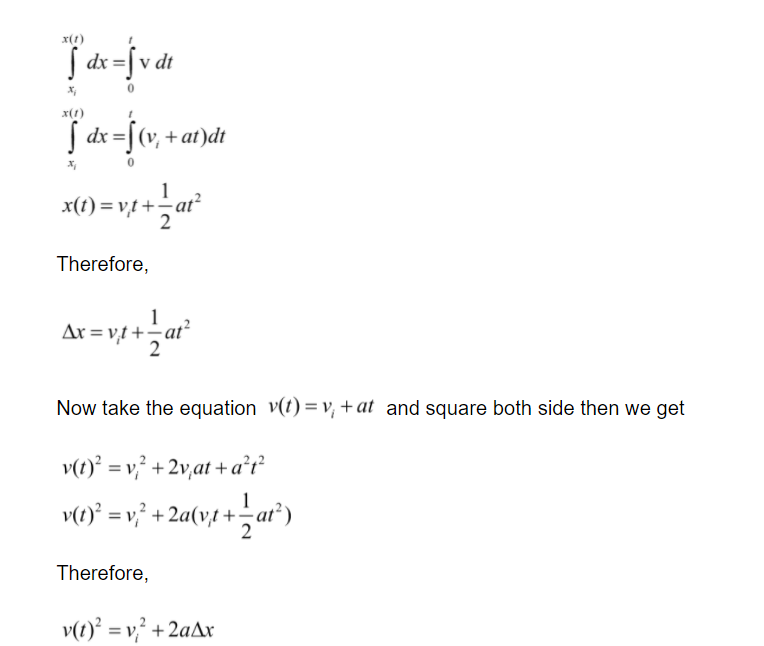
Kinematics in Two Dimensions

Using two-dimensional kinematics in physics, to analyze two-dimensional motion, we resolve all vector components in two directions that are normal to each other. Movement along any of these directions is then free from movement along the other. Consequently, the equations of motion can be applied separately for each of these directions.

Let us consider a ball thrown off the ground at an angle horizontally. The ball experiences a constant acceleration called gravitational acceleration and horizontal acceleration is zero.

Velocities components are

Vector Addition

The process of addition of two or more vectors together is known as vector addition. Depending on the direction of the vector, vector addition is classified into two types

1. Parallelogram Law of Vector Addition.
2. Triangular Law of Vector Addition.

Vector addition method is chosen depending on the arrangement of the head and tail of vectors.

• When two vectors are arranged head to tail then the triangular law of vector addition is applicable
• When two vectors are arranged head to head or tail to tail then the vector addition is performed using parallelogram law

Vector subtraction

Vector subtraction is defined as a process of subtracting the coordinates of one vector from the coordinates of another vector. When subtracting vectors, the direction of the vector to be subtracted must be reversed. This indicates that the length of one vector is subtracted from the other vector.

Vector subtraction of 2 (two) vectors a and b is defined by a-b . It is the addition of negative of vector b to vector a that is a-b=a+(-b) . Hence, vector subtraction includes the addition of vectors and the negative of a vector.

Rotational Kinematics Equation

In rotational kinematics equation

1. Displacement replaces with change in angle (Θ).
2. Initial velocity replaces with initial angular velocity (ω_t).
3. Final velocity replaces with final angular velocity (ω_f).
4. Acceleration replaces with angular acceleration (α).

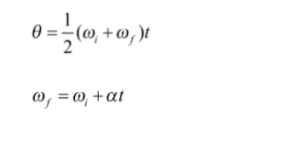
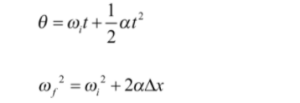
Conclusion

Kinematics is the science that describes the movement of objects using words, diagrams, numbers, graphs, and equations. Kinematics is a part of mechanics. The goal of any study of kinematics is to result in sophisticated mental models which can be used to describe (or explain) the motion of real objects.

The basic kinematics equations are

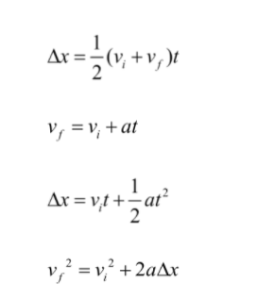
A vector is a physical quantity that has both direction as well as magnitude, like velocity or force.

A quantity which has only magnitude but not direction, like temperature or time, known as scalar.

The distance travelled by a body in a unit interval of time is termed as speed.

Velocity is a Physical Vector Quantity. Velocity has both magnitude and direction also.