Inverse variation is a type of proportionality that on increasing one quantity, the other quantity decreases and vice versa. Moreover, if we dig deep into the concept of indirect variation, we will get to know that the product of two variables in the variation equation will always produce a constant.
For example: When we say that Y varies inversely with X and multiply Y and X together, the product of the two numbers will yield a constant value K. The value of the proportionality constant K in the inverse variation cannot be zero. The constant K is introduced in the proportionality equation when the proportionality sign is removed from the expression.
Definition of inverse variation
Two quantities are said to be indirectly related to each other when the product of these two quantities yields a constant term. This constant term produced by the multiplication of two terms that are indirectly related is called the proportionality constant.
To have a thorough understanding of indirect variation, you need to have in-depth knowledge of ratio and proportion. The ratio is the concept used to compare two or more numbers. A ratio is generally expressed in terms of a fraction. The ratio helps us identify how larger or smaller a number is compared to another quantity. A ratio can be defined as a:b or a/b.
A proportion is an operation that helps you know that two proportions are equal. Astonishingly, a proportion is also known as a variation. Therefore, if we consider that a:b and c:d are equal, then a, b, c, and d are in proportion. Proportions are generally represented as a:b::c:d.
Application of inverse variations
Inverse variation has a considerable amount of effect on our daily life. If we observe, we will realize that the inverse variation has its application in different scenarios in our lives. Some of the places where inverse variation is used are as follows.
- The bank balance is inversely proportional to spending.
- The number of family members is inversely proportional to your savings.
- The number of days required to complete a particular work is inversely proportional to the number of laborers hired.
- The speed of an object is inversely proportional to time. The acceleration of an object is also inversely proportional to time.
- The acceleration of a body is also inversely proportional to the body’s weight.
- The number of failures in a class is inversely proportional to qualified teachers and hardworking.
- The battery power is inversely proportional to usage.
These are examples of inverse variation application in our daily lives. Indirect variation is used in our daily lives whenever we trade off some things.
The formula for indirect variation
The general equation of indirect variation is Y = K×(1/X) or K = XY. Here K is the proportionality constant. The variable X is inversely proportional to another variable Y when Y varies as a reciprocal of X.
Therefore if Y is inversely proportional to X, we can write Y × (1/X) or Y= K × (1/X). Conversely, the expression also stands true. The relationship between variables in the indirect variation is completely opposite of that indirect variation. To properly understand the formula for inverse variation, consider the following example.
For instance, if the speed of a car increases, it will take less time to cover the distance and vice versa. This is due to the relation between speed, time, and distance. Speed is inversely proportional to time. Therefore, as the speed of the vehicle increases, the distance covered increases and the time decreases.
Example questions of inverse variation
After getting thorough knowledge about the different concepts related to indirect proportion, it is now time to solve some inverse variation questions.
- If K/5 = 3 and K/x = 15. Find the value of x when y = 30.
To begin with, we will first solve one of the easier questions on inverse proportion. In this question, we will first solve the first equation to get the value of K. Therefore,

The value of x is 1/2.
- Tell whether y is inversely proportional to x in the table given below. Moreover, if possible, write the equation for the inverse variation.

To solve the values given in the above table for inverse variation, the products of all the pairs of X and Y must lead to the same number. Therefore,

When we multiply all the pairs of X and Y, we know that the constant produced by multiplying is the same, i.e. k = 24. Therefore, the equation for inverse proportionality will be as follows:
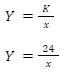
Once you get the proportionality equation, you can draw a graph between Y and X variables. The graph between variables Y and X will be a hyperbola.
Conclusion
In this article, we learned about inverse variation. Apart from learning the mathematical side of the inverse variation, we have also gained knowledge about its applications in real-life scenarios. Inverse proportion is an important concept for different subjects apart from mathematics. The inverse proportion has extensive applications in different subjects such as economics, physics, chemistry, etc.
Moreover, having in-depth knowledge about inverse proportion can help you solve physics problems pretty quickly. The areas where the inverse proportion is extensively used in physics are kinematics, work, energy, electricity, etc.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






