The Gauss law is an extremely important condition that is used to determine the electric field even though it is not directly related to the electric field. Gauss Law is stated as the total electric flux in a given area is the enclosed charge divided by the permittivity. However, the electric flux depends on the electric field because electric flux can be defined as the summation of the electric field lines that can pass a particular area. Thus, utmost importance is given to finding the electric field using Gauss law.
Thus, Gauss law is a link between the total charge enclosed within the surface and the field at all locations on the surface. This may appear to be a clumsy way of putting things, yet it turns out to be a very helpful relationship to determine the electric field. The finding of the electric field using gauss law with examples will give a clear insight into the concept.
Gauss’s Law
Gauss law states that the electric field flux through a closed surface is equivalent to the charge enclosed divided by a constant term called permittivity.
Mathematically, the gauss law can be demonstrated as,
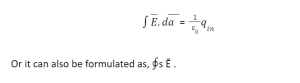
Thus, the statement of the Gauss Law states that the total flux that has been linked by a closed surface is about 1/0 times the charge which has been enclosed by such a closed surface.
From the above-given equation, we can understand that the electric flux will always remain equal to the charge enclosed, regardless of the geometry of the closed surface. Thus, the above-given equation can explain the importance of finding electric fields using Gauss Law.
Examples to find electric fields using Gauss Law
Suppose a point charge q is placed inside a cube having edge ‘a’ then according to Gauss law, the flux through each face of the cube would be about q/60. From the value of this electric flux, the electric field can be calculated easily.
When a charge distribution is supplied, Gauss’s Law can be used to calculate the electric field. Only a limited set of symmetric charge distributions may be applied to Gauss’s Law using analytical equations.
The importance of finding the Electric field using Gauss Law is extremely necessary for understanding electricity. In general, the electric field of a surface is computed using Coulomb’s equation. However, understanding the notion of Gauss law is required to calculate the electric field distribution in a closed surface. It explains how an electric charge is enclosed in a closed surface or how an electric charge is present in a closed surface that is enclosed.
Gauss Law Formula
According to the Gauss Law, the total charge enclosed in a closed surface is in proportion to the total flux that has been enclosed by the surface. Thus, the total electric charge Q encompassed by the surface when the total flux is about , and the electric constant is considered to be 0 is,

Steps to find the Electric Field using Gauss Law
The most important part of finding the electric field using Gauss Law in examples is to select the simplest surface with the simplest spatial symmetry with charge distribution. The symmetry can be spherical, cylindrical or planar.
Afterwards, Gaussian symmetry with similarity to spatial symmetry is to be found.
An integral was to be found along the Gaussian surface, which will be followed by the flux.
The charge that has been enclosed by the Gaussian surface needs to be found.
Ultimately leads to finding the electric field using gauss law with the help of the point charge.
The electric field is governed by a force called the Coulomb force that helps to find out the magnitude and the direction of the electric field. If the field is due to a positive charge, then its direction will be radially outward, and if it is due to a negative charge, then the direction of the electric field will be radially inwards.
Suppose Q is a point charge that has been placed in a vacuum. If we introduce another point charge q at a distance r from the charge Q, then the electric field will become,

Applications of Gauss Law to find the electric field in different examples
Electric Field due to a line charge
Electric fields can be found out easily with the help of Gauss Law.
Suppose a line charge having linear charge density λ is available in the form of a thin charged rod. To find the electric intensity at point P, consider a right circular closed cylinder having an extremely long line of charge as its axis.
The magnitude of the intensity of the electric field shown by each point on the Gaussian surface of a cylinder will appear the same due to the arrangement of all points at the same distance from the line charge.
Therefore, the curved surface of the cylinder contributes towards electric flux is given as,

Where 2rl = curved surface area of the cylinder.
At the ends of the cylinder, the direction shown by the electric field and its angle is about 900. Therefore, these ends of the cylinder will not have any effect on the electric flux.
Therefore, the equation becomes
ϕ E = q/ εo
Charge enclosed in cylinder=line charge density × length
Therefore, the charge enclosed in the cylinder = λ
According to Gauss law,
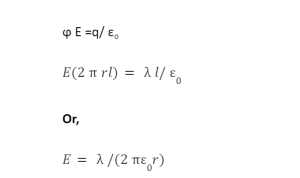
Electric Field due to a Uniformly Charged Sphere
Consider σ to be the uniform surface charge density of a sphere of radius R.
Field seen Outside the Shell
To find out the electric field intensity at a point P outside the spherical shell when OP = r.
The Gaussian surface was taken as a sphere having radius r, while the electric field intensity will remain the same at every point seen on the Gaussian surface.
Thus, Gauss theorem becomes,

Hence, it can be seen clearly that electric intensity at any point that remains outside the spherical shell is such as if the entire charge has its concentration at the centre of the shell.
Field seen at the Surface of the Shell
So total charge enclosed by gaussian surface= qin= A
Total flux = =E(2A) (As the cylinder has two end cap)
Now by applying gauss law we can say that,
E(2A)=10(A)
Or E=20
Here the electric field depends on surface charge density.
Field Inside the Shell
If the point P lies inside the spherical shell, then the Gaussian surface is a surface of a sphere having radius r. Since no charge is present inside the spherical shell, the Gaussian surface encloses no charge. Hence, q = 0.
Thus, the electric field becomes,
E = 0
It proves that the field inside the spherical shell will always be zero.
Conclusion
An electric field is a field associated with each charged particle enclosed in a space. It can be calculated by electric flux, which can be calculated with the help of Gauss Law. Gauss law can be stated as the electric field flux through a closed surface is equivalent to the charge enclosed divided by a constant term called permittivity. We can find out the electric field by Gauss Law in symmetry species, for example, a cylinder, sphere, etc. Thus, the importance of finding out electric fields using Gauss Law can be seen in understanding the concept of electricity.
What is the formula for radius of gyration?
After we have understood the meaning, it’s time to know what is the formula for radius of gyration?
The radius of gyration of a uniform rod is the root mean square distance of the point masses of the object from either its mass’s centre or some other axis, depending on what kind of application it’s for.
A body’s gyradius, or the radius of gyration, is always centred on a rotation axis. It’s defined as the spiral distance between two points with a moment of inertia. When you look at this point’s gyration radius, you can figure out the average distance it has travelled.
The following is the formula for moment inertia in terms of the radius of gyration of a uniform rod:

To know what is the unit of radius of gyration, remember that the radius of gyration is measured in mm.
Consider a system made up of m atoms, each of which has a mass of m. The rotation’s perpendicular distance is represented by r1, r2, r3,… rn from the pivot.
The gyration radius is the root-mean-square distance between the body’s various particles. It comes from the rotational axis and is derived from the rotational axis.
The Radius of Gyration’s applications:
- There is a term called “radius of gyration” that refers to the method used to spread out the many parts of an object around it.
- This is the distance from the rotational axis to a certain point of mass when the object is at rest.
- A two-dimensional range of gyration can be used to show how the cross-sectional zone is spread out in primary design.
- The mass of the body forms a circle around its central point. This is useful to know what is the unit of radius of gyration.
When finding out what is the unit of radius of gyration, the gyratory radius may be determined as:
R=√(IA)
Where I is the object’s second moment of area and A is its entire cross-sectional area.
When the snapshots of the two-dimensional gyration tensor aren’t the same, the gyration radius can be used to figure out the solidity of a piece. There will usually be two heads: one with a smaller head, and one with a bigger head next to it. For instance, the more modest semi-pivot is more likely to lock on to a piece with a curved cross-section than the more powerful full pivot.
The radius of gyration is an important part of the design, and constant groups of the issue are often looked at.
Using the Radius of Gyration
The gyration radius is used to compare the compression behaviour of various structural forms along an axis. A compression beam or member’s buckling can be predicted using this method.
The radius of gyration (two-dimensional) is utilised in structural engineering to show how a column’s cross-sectional area changes as it moves around the body’s mass.
What is the unit of radius of gyration for a column? A column’s gyration radius can be used to estimate its stiffness. To avoid buckling, make sure the two-dimensional gyroscope tensor has equal numbers of primary moments in each of its axes. If a column has an oval cross-section, the smaller semi-axis will tend to buckle.
The radius of gyration is commonly calculated as an integral in engineering, where continuous bodies of matter are typically studied.
What is the unit of radius of gyration of a thin rod?
The moment of inertia (MOI) of any uniform rod of length l and mass M about an axis passing through the centre and making a 90-degree angle to the length is shown as follows:

Conclusion
Thus, we have had a detailed overview of the Radius of Gyration and what is the unit of radius of gyration. To put it simply, the radius of gyration is the distance from the centre of the body to where all its mass is concentrated, in terms of the centre of rotation. This means that the point will also have a moment of inertia. To understand the relationship between gyration radius and inertia, one must first comprehend the rotational axis. It’s simple to locate one if you know the other.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






