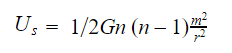Gravitational Self-Energy 

Gravitational self-energy is the amount of work done to create an object of mass M that is formed by joining small masses of mass m which were brought from infinity. Integration has to be performed by considering the potential created for small mass m. It is the energy possessed by the body due to the interactive forces inside the object. This might be described as the work done in assembling all the particles of the body’s indefinite shape and size, or it is the work done in creating a body. The object in gravitational self-energy will always be negative due to attractive forces.  

The formula for calculating gravitational self-energy

Us= -1/2Gn(n-1)m2r 

Where Us= Gravitational Self-energy

G= Universal gravitational constant 

n= number of particles 

m= mass of each particle

r= average distance between two particles 

Gravitation self-energy of a uniform sphere 

Let us evaluate the gravitational self-energy of a uniform solid sphere of mass M and radius R. Since we are now considering continuous mass distribution, the summation goes over to integrals. The calculation is stated below as following:  

Suppose at any moment we have already assembled a sphere at its surface is given by:

ø (r) = G m/r

If we now bring an additional mass element dm to the sphere, the work done in bringing dm form to r is 

dw= (dm) ø (r)= G mdm/r

Corresponding change in potential energy is, dU= -dW= 1-Gmdm/r 

Which is the self energy of a uniform sphere. It is the same as the positive energy required to dissociate the sphere into individual particles and take them to infinity apart. 

Interaction energy of system of particles 

In a system of N particles with masses m1, m2…mn separated from each other by distance r12, r13…. where r12 is the separation between m1and m2 and so on. 

The total collision energy of the system 

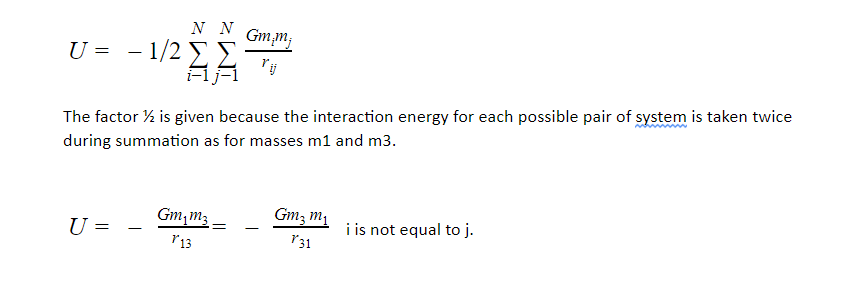
Gravitational self-energy of a system of ‘n’ particles

Let us consider n particle system in which particles interact with each other at an average distance r due to their mutual gravitational attraction; there are n(n-1) /2 such interactions, and the potential energy of the system is equal to the sum of the potential energy of particles which is:

Gravitational Potential Energy 

Work done against gravity in lifting an object is known as the gravitational potential energy of the object Earth-system. The change in gravitational potential energy, ΔPEg, is ΔPEg = mgh, with h being the increase in height and g the acceleration due to gravity. The gravitational potential energy of an object near Earth’s surface is due to its position in the mass-Earth system. Only differences in gravitational potential energy ΔPEg, have physical significance. 

As an object descends without friction, its gravitational potential energy changes into kinetic energy corresponding to increasing speed, so that ΔKE = −ΔPEg. 

Conclusion

Using generalised reciprocity, the mass performing from self-energy is calculated. The mass performing from the gravitational field has a restricted expression. This formula is attained by treating the mass as a little tiny thread and also as a small spherical. Graviton waves propagate as a travelling wave, according to a competent equation for their propagation in space. A new amount formula for graviton energy depending on frequency is deduced by treating gravitational waves as wave packets. This work also quantizes the gravitational constant (parameter). The classical self-energy problem has been studied in the past in connection with the renormalization of a charged point particle. Still, exact solutions have not been thoroughly discussed in the simple framework of Newtonian gravity.