The gravitational field is defined as the strength of the gravitational force. It is also the force that is acting on a unit test mass.
Eg = F/m
Or, Eg = [- [GMm/r² ]/m r
Gravitational Field Intensity (Eg) = [- GM/r2]
Newton proved that the gravitational field in the solid spherical shell is the same at all points of the shell.
Gravitational Field in Different Bodies
Newton’s gravitational law is solely based on point masses. This law’s expression of a particle’s gravitational field serves as a starting point for creating relations of field strength owing to rigid bodies. As a result, mathematical derivation of field strength for geometric shapes is based on a real body mass which accumulates all the collection of discrete elements and combines separate effects. We’ll need to use some visualisation because we’ll be combining vectors with directional properties.
We will also see Newton’s shell theory, which is important to define spherical mass as a point mass, along with these derivations for gravitational field strength.
Celestial bodies that have a discernible gravitational field along with motions lure us to the vast world of science. Our main objective is to derive a mathematical expression for the field strength of a solid sphere. A solid sphere can be seen as an endless number of closely packed spherical shells. The spherical shell, on the other hand, can be seen as a collection of thin circular rings of various sizes.
Finding the net effect of these elements can be a tedious process. As a result, our primary objective is to formulate an integral expression for elemental mass that is suitable for integration between reasonable limits. Now, for the integration process, you need to start from the ring, then move towards the spherical shell, and then proceed to the solid sphere.
Gravitational Field Because Of The Uniform Circular Ring
We need a gravitational field that starts from the point plying from the central axis of the ring. In the figure given below, the gravitational field is measured in the axial point “P”. Here, “M” would be the mass and “a” would be the radius. There also lies a small mass “dm” on this circular ring.
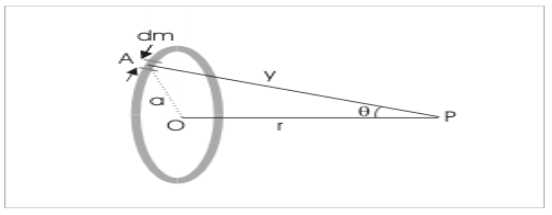
dE = Gdm / PA²
= Gdm / (a² + r²)
The following figure shows that the gravitational field is axial. This gravitational field is shown in the plane of OAP in directions parallel and perpendicular to the axis.
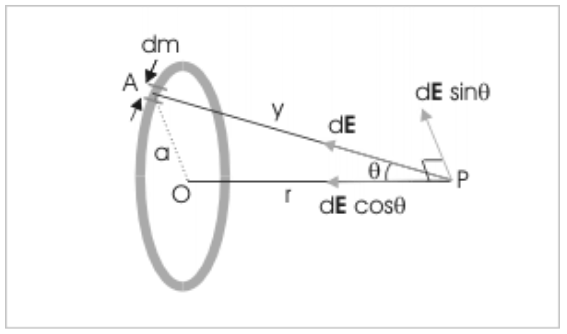
Devi = dE cos ∅
dEī = dE sin ∅
There are two points to consider when derivating the value.
First, the figure shows the measurements of “y” and “r”, which are the same for all elemental masses. Also, you need to examine elemental masses that are equal. All these elements of mass “dm” are equidistant from point “P,” and the magnitude of the gravitational field due to this is the same.
Second, with the pair of elemental masses on symmetrically opposite sides of the ring, the perpendicular components of elemental field intensity are directed in opposite directions. These perpendicular components will become zero for the entire ring when the integration is done. If the mass distribution on the ring is uniform, we may say that zero-field strength is perpendicular to the axial line. For obtaining the uniform ring of the net gravitational intensity, we have to integrate the axial components of the elemental field strength only.
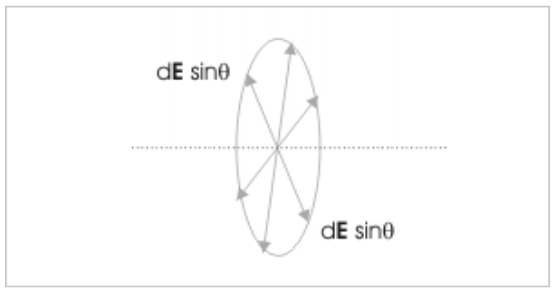
In the preceding figure, the perpendicular components will cancel each other.
Hence, the mathematical expression would be:
E = ∫ dE cos ∅
E = ∫ Gdm cos ∅ / (a² + r²)
Here, cos ∅ represents the trigonometric ratio, which is constant for each point on the circular ring. Now, take out the cosine ratios along with other constants from the integration.
E = G cos ∅ / (a² + r²) ∫ dm
Now, after integration, m = 0 to m = M
G M cos ∅ / (a² + r²)
For triangle OAP,
Cos ∅ = r / (a² + r² ) ½
Now, substitute the values of cos ∅ in the equation:
E = GMr / ( a² + r² ) 3/2
E = 0 when r = 0
At the centre of the ring, the gravitational field will become zero. This is due to the gravitational forces produced by two opposed identical elemental masses that are equal and opposing, balancing each other.
Gravitational Field Due To A Uniform Solid Sphere
The uniform solid sphere with radius “a” and mass “M” is made up of an unlimited number of thin spherical shells. If you see the figure given below, one such spherical shell has an infinitesimally small thickness “dx.” The strength of the gravitational field because of the thin spherical shell, which is placed outside the shell at a linear distance “r” from the centre, is given by:
dE = Gdm / r²
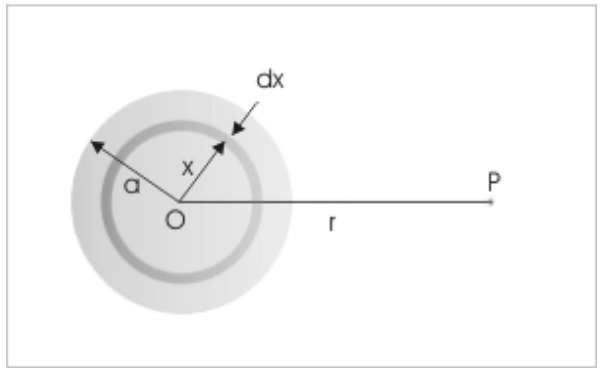
In the preceding figure, the gravitational field is at a distance ‘r’ from the centre of the sphere.
The gravitational field strength produced here acts in the direction of the sphere’s centre. You can also add gravitational field strengths of different shells to obtain the sphere’s field strength. Here, you can note that the centres of all-spherical shells coincide at one point. It also means that the spherical shells have the same linear distance between their centres and the point of view. You can deduce that “r²” is constant for all spherical shells and can also be removed from the integral.
E = Gdm / r² = G/r² ∫ dm
= GM / r²
A uniform solid sphere behaves just like a shell in the equation given. It acts as though all of its mass is concentrated in its core for a point outside. The radius of the sphere, “a”, is part of this equation. But, the point outside of the sphere acts as a point mass.
Conclusion
Thus, from the above mathematical equations, we can deduce that the gravitational field is the gravitational force per unit mass, i.e., a tiny mass would exist anywhere. It is a vector field that points in the direction of the force experienced by the mass.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






