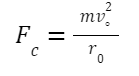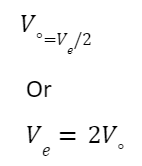Escape Velocity and Orbital Velocity

The lowest speed required for a free, non-propelled object to escape from the gravitational pull of a main body and reach an infinite distance from it is known as escape velocity or escape speed in celestial mechanics the escape speed increases with the mass of the primary body and decreases with distance from the primary body.

Escape Velocity

“The speed at which a body must travel to escape the gravitational field of the earth.” This is owing to the downward force of gravity. The item soars to a larger height with enhanced initial velocity before returning. If we continue to increase the starting velocity of the object, it will eventually stop returning to the ground. It will be able to escape gravity’s clutches. The initial velocity at which an object exits the earth’s gravitational field is referred to as E.V.

Escape velocity formula

The E.V. represents the body’s initial kinetic energy, which propels it to an infinite distance from the earth’s surface.                       

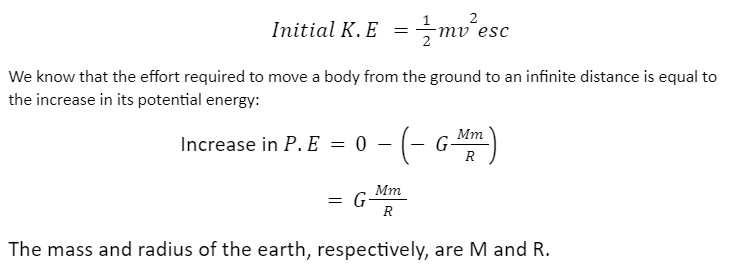
Orbital velocity

The motion of an object in the earth’s orbit is known as orbital motion. Orbital velocity is the rate at which an object moves around the earth’s orbit. In the gravitational field, it remains constant. The earth, along with some other planets, orbits the sun in a nearly round course. Human-launched artificial satellites follow a nearly circular path around the globe as well. Orbital motion is the name for this type of movement. This velocity’s formula is as follows:

Consider a satellite travelling in a circular path around the planet. The satellite’s mass is m, and its orbital speed is vo. The mass of the Earth is M, and the radius of the orbit is r°. To keep a satellite in orbit, a centripetal force is necessary, which is calculated as:

Overview

The presence of escape velocity is a result of energy conservation and a finite depth energy field. When a moving item has a particular total energy and is subject to conservative forces (such as a static gravity field), the object can only reach combinations of locations and speeds that have that total energy; places with a higher potential energy cannot be reached at all. Increasing the object’s speed (kinetic energy) widens the range of feasible destinations until, with enough energy, they become infinite.

Relation between escape velocity and orbital velocity

The following is the basic distinction between escape velocity and orbital velocity: Escape velocity is the speed at which a body must travel to escape the gravitational field of the earth. It has a speed of 11 km/s. The velocity necessary for a satellite to move in Earth’s orbit is known as orbital velocity. It has a speed of 8 km/s or 29000 km/h.

In astrophysics, the relationship between escape velocity and orbital velocity is given as:

Where,

Ve is the Escape velocity measure using km/s.

Vo is the orbital velocity measure using km/s.

We know that Escape velocity =2× Orbital velocity, implying that the escape velocity is proportionate to the orbital velocity. For anybody with a large body, this means:

• When the orbital velocity increases, so does the escape velocity, and vice versa.

• If the orbital velocity falls, the escape velocity will fall as well, and vice versa.

It’s important to note that this escape velocity is related to a non-rotating frame of reference, not to the planet’s or moon’s moving surface, as we’ll see later.

From a rotating body

The direction in which an escaping body travels affects its escape velocity relative to the surface of a rotating body. Because the Earth’s rotational velocity at the equator is 465 m/s, a rocket launched tangentially from the equator to the east needs an initial velocity To escape, a rocket launched tangentially from the equator to the west needs an initial velocity of about 10.735 km/s relative to the moving surface at the time of launch, whereas a rocket launched tangentially from the equator to the west needs an initial velocity of about 11.665 km/s relative to the moving surface at the time of launch.

From an orbiting body

At a particular height, the escape velocity is display style sqrt 2 times the speed in a circular orbit at the same height (compare this with the velocity equation in circular orbit). This is because an object in such an orbit has a potential energy of minus two times its kinetic energy with regard to infinity, whereas the sum of potential and kinetic energy must be at least zero to escape. The first cosmic velocity is sometimes referred to as the circular orbit velocity, whereas the escape velocity is referred to as the second cosmic velocity in this context. 

Conclusion

The minimal velocity required to overcome a big body’s gravitational potential and escape to infinity is called escape velocity. The velocity with which an object circles around a huge body is known as orbital velocity. The orbital velocity and escape velocity have a proportional relationship.