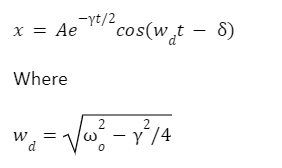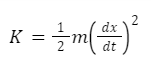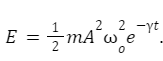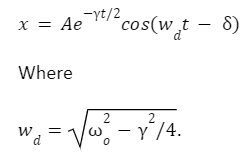Energy Of A Weakly Damped Oscillator

Damping forces are a particular type of force used to slow down or stop a motion. The critical point is that damping forces only work on vibratory motion or on systems that exhibit an oscillatory nature. It is a force that restricts vibrations that can be mechanical or electrical. The damping effect caused by damping forces is due to the dissipation of energy.

Any damping force in an oscillatory system aims to decrease its oscillation frequency or prevent the oscillation from happening. Damping is an effect that is caused by damping forces and occurs in almost every system. For damping to not occur in a system, it has to be free of any forces that oppose the oscillatory motion of the force. Such a system is possible in classical mechanics. Every applied force receives a response, acting as the damping force.

Levels of Damping

There are different levels of damping that can happen on a system;

• Undamped

An oscillatory system that oscillates so that no energy is lost in any oscillation is called an undamped system; since there is no damping force acting on the system. Such a system will keep oscillating for infinite time without ever stopping. 

• Underdamped

A perfectly undamped oscillatory system is not possible. There is always a damping force acting on an oscillatory system. When this damping force is such that the oscillations gradually tend towards zero oscillation, then the oscillatory system is said to be underdamped. In an underdamped system, the oscillating body may pass its starting position more than once, but it loses energy and eventually stops oscillating with every oscillation.

• Critically damped

Frequently, it is required that the system be brought to rest as soon as it is put into oscillation. For example, when a bike passes over a speed bump, the suspension begins oscillating but stops after a momentary time. In order to achieve damping such that the oscillation of a body stops as soon as it starts oscillating, the system has to be critically damped. In the example of the bike, the suspensions are critically damped either mechanically or by adding a viscous liquid that prevents the suspensions from oscillating for too long.

• Overdamped

If a door with proper damping is swing very hard, it is noticed that the door closes smoothly without swinging back. When an oscillatory system is damped so that the oscillating body never crosses the starting point of its oscillation, that system is said to be overdamped. In an overdamped system, oscillations continue for a while, but the oscillation amplitude is always less than the initial amplitude. The difference between overdamping and critical damping is that critical damping focuses on not allowing oscillations to happen at all. In comparison, overdamping focuses on the oscillation amplitude to sharply decrease.

Introduction to a Damped Oscillator

Any system that periodically repeats a to and fro motion is said to be in oscillation. A system that has an oscillating body is called an oscillator. Let us take an oscillator created by attaching a spring to a box. When the box is tugged and the system is put into oscillation, the system infinitely oscillates until stopped by external force in an ideal system.

However, when the box oscillates freely, it is observed that it stops oscillating after some time. It is due to the damping forces acting on the oscillator. When the damping forces are such that the oscillator is underdamped, it is called a weakly damped oscillator. The damping force is given by;

F=-p×dx/dt, where p is the viscous coefficient of the damping force.

The displacement in a weakly damped oscillator is given as

Here, d gives the rate of damping of the system, and o is the angular velocity of the system when there is no damping force acting on it.

Where A and are two constants dependent on the initial condition of the oscillator. The velocity of the oscillator is given as,

Energy of a Weakly Damped Oscillator

Now that we know the velocity and displacement of a weakly damped oscillator let us calculate the energy of a weakly damped oscillator. Let m be the mass of the oscillating body, then the kinetic energy of the oscillator at any given time is given as,

The cosine component can be ignored for a weakly damped oscillator as it is not significant. Hence, the total energy of a weakly damped oscillator is given as;

Conclusion

The damping force is given by,

F=-pdx/dt , where p is the viscous coefficient of the damping force.

The displacement in a weakly damped oscillator is given as,

Here, ω d gives the rate of damping of the system, and o is the angular velocity of the system when there is no damping force acting on it.

Where A and are two constants dependent on the initial condition of the oscillator. The velocity of the oscillator is given as;

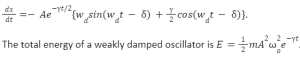
The total energy of a weakly damped oscillator is E=12mA2o2e–t.