Profile
Settings
Refer your friends
Sign out
The Gauss law is a fundamental concept in electromagnetic and physics. It’s utilised to connect the charge distribution to the ensuing electric field caused by the charge. Joseph Lagrange proposed this law in 1773, followed by Carl Gauss in 1813. This law was developed by both of them in the context of the attraction of ellipsoids. One of Maxwell’s four equations, which provide the foundation for classical electrodynamics, includes this law.
Gauss’s law, often known as Gauss’s flux theorem (or just Gauss’s theorem) in physics and electromagnetic theory, is a law that relates the distribution of electric charge to the resulting electric field. It asserts that the flux of the electric field out of any closed surface is proportional to the electric charge enclosed by the surface, regardless of how that charge is distributed, in its integral form. Even while the law by itself is insufficient to estimate the electric field across a surface encompassing any charge distribution, in circumstances where symmetry requires uniformity of the field, this may be possible. In the absence of such symmetry, Gauss’s law, which states that the divergence of the electric field is proportional to the local density of charge, can be employed in its differential version.
Electric Flux
Consider a liquid moving over dS surface with a velocity of v. The rate of liquid flow across the surface is represented by vdS. This is the liquid flux that is moving through the surface. In a similar fashion, the flow of the electric field is defined. It’s known as the electric field flowing through a small area patch dS. The patch’s size is proportional to the number of electric field lines that pass across it.
E.∆S
Here,θ is the angle
E.∆S cosθ
Flux is
ϕ=E.∆S cos
Gauss’s Law
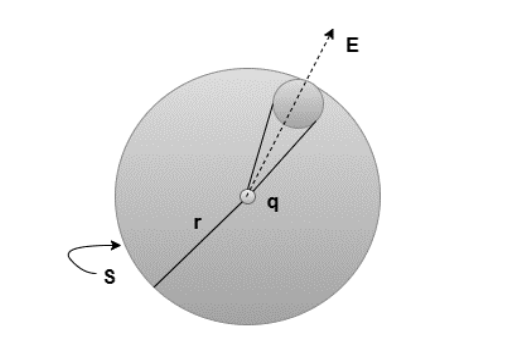
Consider a small charge q enclosed in a sphere with a radius of r. This sphere can be divided up into smaller area portions, as shown in the diagram below. The following equation will be used to compute the electric field that flows through the element:
ϕ=E.∆S= q ⁄ 4πϵr2r. ∆S
Electric Field due to Infinitely Long Straight Wire Derivation
Gauss’s law can be applied to a variety of charged forms to generate the equations for an electrical field. Consider a charge carried on an infinitely long wire. lambda represents the charge per unit length of that wire. The wire has a symmetry axis, which is seen in the diagram below. The goal is to find an equation that may be used to calculate the electric field generated by this wire.
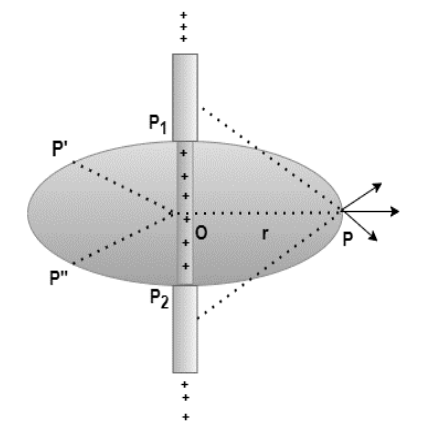
Consider a radial vector OP that has been spun around the wire. This indicates that the electric field at all places P, P’, and P” must be the same. If the charge is positive, the electric field is radially outwards; if the charge is negative, the electric field is radially inwards.
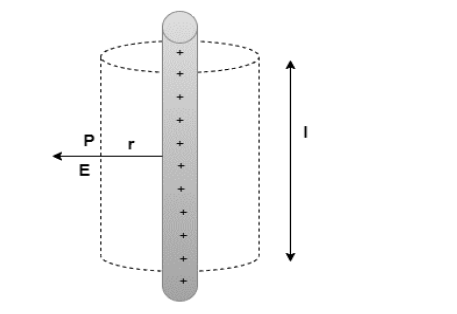
Calculate the electric field using a cylindrical Gaussian surface. Because the field is radial everywhere, flux along the two faces of the cylinders is zero. E is perpendicular to the surface at each point on the cylindrical part of the surface, and its magnitude is constant because it relies only on r. The curved part’s surface area is 2πrl, where l is the cylinder’s length.
Flux via the curved section of the cylinder Equals flux across the surface
=E × 2πrl
A charge equal to λl is enclosed by the surface.
E × 2πrl= λl ⁄∈
E=λ ⁄ 2πrɛ
Conclusion
In electrostatics, the ultimate goal of Gauss’s law is to find the electric field for a given charge distribution enclosed by a closed surface. It is the most important electromagnetic law.
Gauss’ Law can be utilised to solve electrostatic problems with unusual symmetry, such as cylindrical, spherical, or planar symmetry. The following is how we use Gauss’s Law:
- Choose a Gaussian surface that makes evaluating the electric field simple.
- To make tasks easier, apply symmetry.
Gauss’s law is mathematically comparable to several other laws in physics, including Gauss’s law for magnetism and Gauss’s law for gravity. Gauss’s law can be formulated similarly to any inverse-square law: for example, Gauss’s law is essentially comparable to the inverse-square Coulomb’s law, and Gauss’s law for gravity is essentially equivalent to the inverse-square Newton’s law of gravity.
