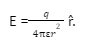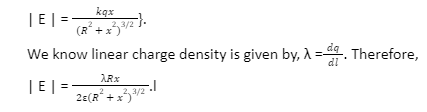Electric field intensity can be determined by the amount of electric force experienced by a test charge q₀ in the presence of the electric field.

Electric field intensity due to a single charged particle is given as,

We can find an electric field at any point, due to a charged object, by identifying the type of charge distribution.

Types of Charge Distribution

• Linear Charge Distribution

If the charge is distributed linearly over a body, it is called linear charge distribution.

λ = dq/dl

λ = linear charge density

dq = charge

dl = line element

• Surface Charge Distribution

If the charge is distributed continuously over the surface of a body, it is called surface charge distribution.

σ = dq/ds

σ = surface charge density

dq = charge

ds = surface element

• Volume Charge Distribution

If the charge is distributed continuously over the volume of a body, it is called volume charge distribution.

ρ = dq/dv

ρ = volume charge density

dq = charge

dv = volume element

Electric Field Intensity at Any Point on the Axis of a Uniformly Charged Ring

Let us consider a circular ring of wire with zero thickness and a radius R. +q is the charge on the ring, distributed uniformly over the ring’s circumference. We have to determine the electric field intensity at any point P on the axis of the loop, which is at a distance x from the centre of the ring O.

Let AB be the length of element dl.

The charge on the element AB is, 

dq =qdl/2πR 

Electric field intensity at P due to charge element AB is,

|dE| = K dq/(CP)2

where, K = constant = 14,

|dE| =K dq/(R2 + x2) 

Now, resolve electric field intensity dE into two rectangular components, that is

dE cosθ along the x-axis and dE sinθ along the y-axis.

For the pair of diametrically opposite elements of the charged ring, perpendicular components of the electric field intensity will cancel each other. That is,

∫dE sinθ = 0.

Whereas components along the axis of the charged ring will be integrated. That is,

∫dE cosθ.

Hence, the resultant electric field intensity E at P is | E | = ∫dE cosθ

The direction of E is along the positive x-axis of the loop.

Special Cases

1. When point P lies at the centre of the loop

x = 0, therefore,

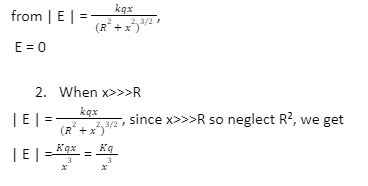
This is the formula for electric field E at a distance x from a point charge.

Hence, a uniformly charged ring behaves as a point charge when the observation point is at a considerable distance from the charged ring compared to the ring’s radius.

Further Notes

• The electric field intensity at the centre of the charged ring is zero.

• A tangent drawn at any point in the electric field line gives the direction of the electric field at that point.

• Electric fields originate from positive charges and terminate in negative charges.

• In electrostatics, the electric field is conservative in nature.

• ∇ × E = 0, where E is conservative.

• Electric field lines are always continuous.

• No two electric field lines intersect each other.

• The formula for electric field intensity at a point passing through the centre of a charged ring is given by:

• Electric field intensity is oppositely symmetrical to the square of the distance between the source and test charges.

Conclusion

Electric field intensity can be determined by the amount of electric force experienced by a test charge q₀ in the presence of the electric field. The formula for electric field intensity anywhere on the axis of a uniformly charged ring is given by:

Electric field intensity at the centre of the charged ring is zero, as all the electric field components cancel each other. When the observation point is at a considerable distance from the charge ring, the charged ring behaves like a point charge.