There are several examples of bodies performing circular motions every day in our daily lives. From the hands of a clock to a car turning on a banked road, there’s a lot to see. Circular motion can be seen in all of these cases. There are two types of circular motion: uniform circular motion and non-uniform circular motion. It is critical to understand the dynamics and equation of the body in circular motion. These dynamics enable us to study these motions and produce statistics relating to the body’s behaviour while in motion.
Circular Motion
A circular motion is defined as an object travelling in a circular route around a point. An automobile turning on the road, for example, is moving in a circular manner around a point. Periodic motions are those that reoccur after a particular amount of time has passed. This motion can be categorised into two groups based on its velocity and acceleration –
- Uniform Circular Motion- Uniform Circular Motion occurs when a body moves in a circular motion at a constant speed along the circle of the circular trajectory.
- Non-Uniform circular motion- When a body moves in a circular motion around the circle of a circular trajectory, the speed of the body changes. This is known as a non-uniform circular motion.
Right-Hand Rule
It states that if the fingers are curled in the direction of motion as if they are gripping the axis of rotation. The direction of the angular displacement vector is represented by the thumb held perpendicular to the curvature of the fingers.
It has a velocity since it moves in a circle, and that velocity is the angular velocity.
The rate of change of angular displacement is known as angular velocity. It is represented by the symbol ω.
ω=v/r
v=velocity
r=radius of the path
Dynamics of Circular Motion
The body moves at a constant speed in this motion. Let’s imagine the body’s speed is v m/s and the radius of the circular trajectory on which it is going is “r.” In time “t,” the body moves from point A to point B as shown in the diagram. The letter “s” stands for the length of the arc from point A to point B. The angle covered by the item is indicated by θ, in this case.
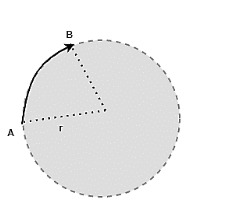
θ=AB/r= s/r
The rate of change of angle is defined as the angular velocity of the body. In the case of straight-line motion, it’s similar to velocity. The Greek letter omega (ω) is used to represent it.
ω=dθ/dt
Now we can use the value of θ in the above relation
ω=d/dt(s/r )
ω=ds/dt(1/r)
The velocity, v=ds/dt
Therefore,
ω=v/r
Uniform Circular motion
The human body has a natural tendency to travel in a straight path. There must be some force that keeps the bodies moving in a circular direction at a constant pace. The centripetal force is the name for such a force. Centrifugal force is the reaction of this force. This indicates that both forces are equal in magnitude and direction.
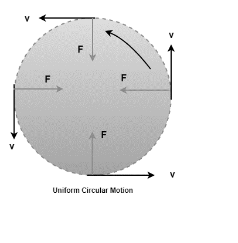
Centrifugal force can be given as,
F=mv²/r
We know that ω=v/r
F=m(ωr)²/r
F=mrω²
Centripetal force
Mechanical arrangements are difficult to meet the special demand of a continuously changing radial force. The condition specifies that the force must change direction in perfect sync with the particle. It’s a difficult task. This is especially true if we consider manipulating force by physically altering the mechanism that applies it.
Fortunately, natural and many cleverly devised arrangements generate scenarios in which the force on the body changes direction when the particle’s position changes – simply by moving. One such arrangement is the solar system, in which the planet’s gravitational attraction is always radial.
The force essential for circular motion is known as centripetal force. Centripetal force is the net component of external forces that meet this criterion. Centripetal force, in this sense, is not an independent force. Rather, we should consider this force as a component of the radial external forces acting on the body.
Direction of centripetal force and circular trajectory
Circular motion has a subtle point in terms of the direction of force imparted to the particle in circular motion. When a particle is at rest, it moves along the direction of the applied force rather than perpendicular to it. The situation is different in circular motion.
We impart centripetal force to a particle that is already travelling in the opposite direction of the force. As a result, the resulting motion from the interaction of motion with external force is tangential rather than radial.
The particle accelerates in the direction of centripetal force, i.e., towards the centre, according to Newton’s second law of motion. As a result, the particle has a downward displacement (Δy) with centripetal acceleration while also moving sideways (Δx) at a constant speed, because the component of centripetal force in the perpendicular direction is zero.
It may seem strange, but the particle is constantly descending towards the centre in the direction of centripetal force while also maintaining its linear distance from the centre due to persistent sideway motion.
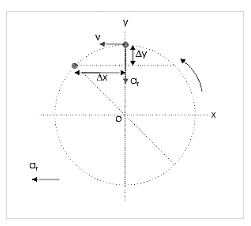
In the diagram, the particle goes towards the centre by Δy, while moving left by Δx at the same time. The vertical and horizontal displacements in the given period are such that the particle is always on the circle as a result of the resultant displacement.
∆x=v∆t
∆y=1/2ar∆t²
Conclusion
Circular motion can be both uniform and non-uniform. It is uniform circular motion if the tangential component of acceleration is absent, and it is non-uniform circular motion if the tangential component of acceleration is present. In the context of non-circular motion, the particle’s net acceleration is the sum of its radial and tangential accelerations.
Assume you’re in an inertial frame of reference and you’re watching a circularly moving particle. Because the particle has some acceleration, the net force on it must be non-zero, according to the second equation of motion. Take, for example, uniform circular motion. The particle’s speed is constant.
Centripetal force is defined as a force that is directed towards the centre. To keep the item in a uniform circular motion, this centripetal force is required. This is just the name given to this type of force, which can be caused by tension, friction, or other factors.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






