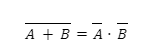A set of two laws which were given by a nineteenth-century British mathematician, Augustus De Morgan, are referred to as De Morgan’s theorem. The two laws use the rules for AND, NOT and OR functions. Using the properties of these functions, one Boolean expression can be converted from one form to the other. The first theorem states that the inversion of the product is the same as the sum of the inversions. The second theorem states that the inversion of the sum is the same as the product of the inversions. De Morgan’s theorem holds true for two or more variables.
The first theorem
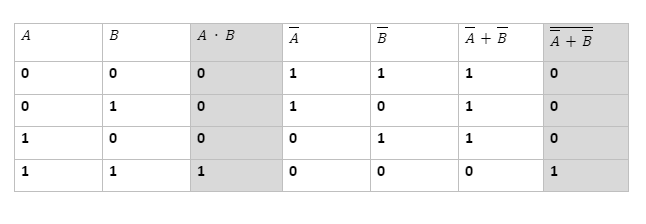
According to the first theorem given by De Morgan, when two or more variables are AND and then complemented, it is equal to the OR of the complement of each variable individually. The first De Morgan theorem can be written as:
Verifying the first De Morgan’s theorem using a truth table
Implementation of the first theorem
Proof of the first theorem
![]() The second theorem
The second theorem
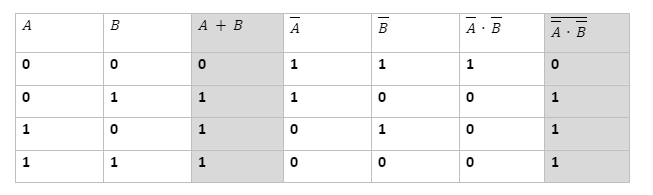
According to the second theorem given by De Morgan, when two or more variables are OR and then complemented, it is equal to the AND of the complement of each variable individually. The second De Morgan theorem can be written as:
Verifying the first De Morgan theorem using a truth table
Implementation of the second theorem
Proof of the second theorem
Simplification using De Morgan’s theorem
To simplify an expression using the De Morgan theorem, use the following steps:
Replace ‘OR’ with ‘AND’ and ‘AND’ with ‘OR’. In other words, replace ‘+’ with ‘⋅’ and ‘⋅’ with ‘+’ given in the expression.
Complement each term in the expression
Example 1
Example 2
Equivalent gates using De Morgan’s theorem
To obtain equivalent gates using De Morgan’s theorem, replace the AND gate with OR gate and vice versa. Also, invert every input and output of the gate. Let us look at some examples of De Morgan’s theorem.
Example 1
Let us take a basic AND gate as follows:
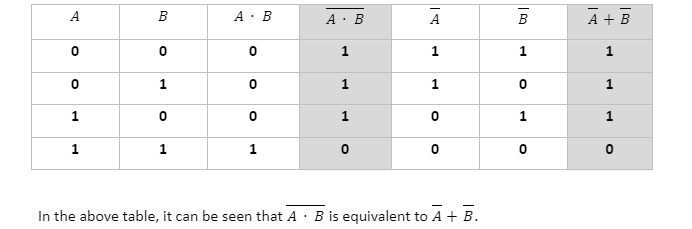
To find an equivalent gate, replace the AND gate with OR gate and invert the two inputs and one output using a NOT gate as follows:
(The bubbles at the input and output represent inversion.)
Let us verify if the above expressions are equivalent using a truth table as follows:
Example 2
Let us take a basic OR gate as follows:
To find an equivalent gate, replace the OR gate with AND gate and invert the two inputs and one output using a NOT gate as follows:
(The bubbles at the input and output represent inversion)
Let us verify if the above expressions are equivalent using a truth table as follows:
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out





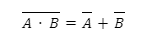

 The second theorem
The second theorem