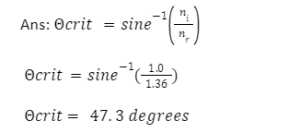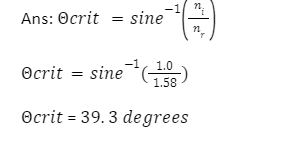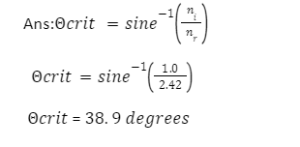Critical Angle and Refractive Index

In optics, the critical angle is the incidence angle at which the angle of refraction is 90 degrees. The ratio of the velocity of a light beam in the air to the velocities of the specified medium is known as the refractive index. Because the critical angle is inversely proportional to the refractive index, it is possible to determine the relationship between the critical angle and the refractive index.

• The angle of incidence above which total internal reflection occurs (optics) is known as the critical angle.

• In aerodynamics, the critical angle of attack is the angle of attack that produces the highest lift coefficient.

• In engineering, the critical angle of repose is the sharpest angle of descent of a slope when the material is about to slide.

The critical angle definition explains refraction rules and how to adjust the angle of incidence to get a 90-degree refraction angle. In order to properly understand the critical angle formula, we’ll also go through Snell’s law. Let’s get this celebration started, shall we?

The law of refraction, sometimes known as Snell’s law, is well-known. Another name for it is the Snell-Descartes law.

In optics, a substance’s refractive index (also known as refraction index or index of refraction) is a dimensionless statistic that describes how quickly light flows through it. It’s described this way:

n=c/v

v is the phase velocity of light in the medium, and c is the speed of light in vacuum. Water, for example, has a refractive index of 1.333, which means light travels 1.333 times slower in water than in air. When the refractive index of a substance is increased, the speed of light in the material decreases.

Critical angle

The critical angle in optics is the largest angle at which a beam of light travelling through one transparent material can contact the border between that medium and a second of lower refractive index without being entirely reflected within the first. (The refractive index of a transparent substance is the ratio of light’s speed in a vacuum to its speed in that substance.) For any angle of incidence smaller than the critical angle, and for any angle at all if the ray contacts the boundary from the other side, a portion of the beam will pierce the barrier, being refracted in the process.

If the angle of incidence is greater than this critical angle, the refracted beam will be reflected back into the medium rather than emerging from it. Total internal reflection is the term for this.

The following are the prerequisites for total internal reflection:

1. Light is travelling from a denser optical media (higher refractive index) to a denser optical medium (lower refractive index) (lower refractive index).

2. The incidence angle is larger than the critical angle.

Each set of media has its own critical perspective. Light going from glass to air, for example, has a critical angle of 42°, while light moving from water to air has a critical angle of 48,8°.

Refractive index

The refractive index, commonly known as the index of refraction, is a measurement of how much a ray of light bends when it passes through one medium and into another. If I is the angle of incidence of a ray in vacuum (the angle between the incoming beam and the normal, which is perpendicular to the surface of a medium), and r is the angle of refraction (angle between the ray in the medium and the normal), The refractive index n is equal to the ratio of the sine of the angle of incidence to the sine of the angle of refraction; in other words, n = sin I / sin r. The velocity of light c of a particular wavelength in empty space divided by its velocity v in a substance, or n = c/v, is also known as the refractive index.

Critical Angle and Refractive Index Equation

The following formula can be used to calculate the relationship between critical angle and refractive index:

Take a look at a ray of light,

• Let I be the crucial angle of incidence C.

• Let r=90o be the refraction angle.

• The rarer medium’s refractive index should be a.

• The denser medium’s refractive index should be b.

What is refractive index of diamond

The refractive index of diamond is given,

d=2.42

Diamond has a 2.42 refractive index.

Conclusion

We used the example of light flowing through water towards the boundary with a less dense material, such as air, in our introduction to TIR. The refracted beam lies along the boundary with a 90-degree angle of refraction when the angle of incidence in water reaches a critical threshold. The critical angle is the maximum angle of incidence for which refraction is still possible. Light will undergo entire internal reflection at any angle of incidence larger than the critical angle.

As a result, the critical angle is defined as the angle of incidence that produces a 90-degree angle of refraction. Keep in mind that the critical angle is a value of angle of incidence. The crucial angle for the water-air interface is 48.6 degrees. The critical angle for the crown glass-water barrier is 61.0 degrees. The critical angle’s actual value is determined by the materials that are present on both sides of the boundary.