Profile
Settings
Refer your friends
Sign out
In a physical system, the centre of mass is a point where the system’s total mass is believed to be concentrated. When the external force is applied to the system, it moves so that its mass is concentrated at that point. To understand the centre of mass in a two-particle system, we consider a system of two identical particles. For a system of two identical masses, the centre of mass lies precisely at the midway point from both systems.
Centre of Mass
In a physical system, the centre of mass is that point within the system, where the system’s total mass is believed to be concentrated. If all the forces acting on the system were to be applied at its centre of mass, the body should remain unaffected. This means whether the system was in rest or motion, the body’s relative position will remain unaffected. If we consider a system of two identical particles with identical masses, the centre of mass of two systems is located exactly at the midway point from the systems.
Significance of Centre of Mass
The centre of mass makes an essential factor in the system’s mechanics. The centre of mass helps in understanding the motion in rigid bodies. In calculations for the centre of mass of a system, we assume a ‘Point Mass.’ Point mass is described as that assumed small object within the system where the system’s centre of mass exists.
If there are two systems of particles with masses m1 and m2 and position vectors r1and r2, then the position vector of the centre of mass is given by,
Note: If two particles have the same mass, then the centre of the mass lies at the midpoint of the line, joining them.
For a system of n particles of masses m1, m2, m3, …. mn and their respective position vectors; the position
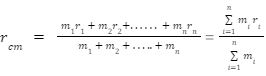
Centre of mass of the two-particle system
Centre of Gravity
The centre of gravity is an imaginary point of an object, on which the force of gravity acts.
Usually, in a mechanical problem, the gravitational field is considered uniform. Therefore, the centre of mass and gravity are at the same point.
Centre of Mass for Three Particles at Different Positions
In some instances, the centre of mass of a system may not lie on the same plane. In a rigid or uniquely shaped body, the centre of mass of all particles may not lie in the same plane. To determine the centre of gravity in a two-particle system, we consider a system of two identical particles. However, it is a system of three particles placed at different positions; the calculations are different.
This equation resembles the equation for the centroid of a triangle. It can be determined that the Centre of mass for a three-particle system lies at the centroid of the triangle formed by the particles.
Conclusion
The Centre of mass of a system is a point within the system, where the system’s total mass is believed to be concentrated. The methods to determine the Centre of mass may differ as per the position of particles in the body. In a two-particle system, we consider a system of two identical particles to determine the centre of mass. In a three-particle system, the Centre of mass lies at the centroid of the triangle formed by these particles.
