The Latin (or Greek) words “centrum” and ” gravitation ” are the origins of the word “centrum” and ” gravitation.” Gravity is the weight, or attractive force, between particles in the cosmos that causes celestial bodies to move, and the centre (centroid) is the centre of mass in the middle of the body’s diagonals.
Centre of gravity
A centre of mass, also known as a barycentre (from the Greek word barrio, which means “heavy”), is the point of an item or system of material points (in R, R, R1, or R2) in which the object’s entire mass is concentrated. This idea permits the entire thing to be seen as a single material point with a mass equal to the body’s total mass. Any system of material points has a centre of mass, regardless of whether or not a force is operating on it. The location where the gravitational force acts on the body is called the mass centre.
Equation
w- total weight of the object.
d-increment of weight.
(We can obtain z by imagining the coordinate system, with the particles fixed in it, as being rotated 90 degrees about the x (or the y) axis).
Knowing w=mg, if we assume that the acceleration due to gravity (g) for every particle is constant (g will be cancelled out)
The centre of mass can also be found outside the mass boundaries of the body, depending on its shape. The triangle’s centre of gravity is in the cross section of the angle bisectors, while the cube’s centre of gravity is in the cross section of its diagonals. The centre of gravity of irregular geometric bodies is found at the intersection of the gravity lines. This is the point where the total external force is operating on the particle system or the body, and it is at an average distance from all the particles of the system or individual body particles. If a particle or body system moves under the influence of an external force, the point at which the centre of gravity is located moves as if it contains all the mass of the system or body. If the body is not with uniform density, the centre of mass (gravity) does not have to be in the geometric centre of the body.
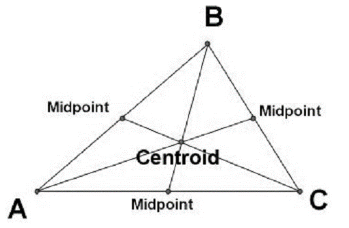
Centroid
The geometric centre is known as the centroid. Simply put, when the body is homogeneous, the centroid corresponds to the centre of gravity (with constant density). The focus point of the vectors’ collection of the gravitational acceleration of all the material points of the same item is defined as the centroid of a body in physics. This point is found at the junction of the gravitational lines if the body is homogenous, and it is defined geometrically in right geometric bodies. Archimedes was the first to describe the method for determining an object’s centroid. He suggested cutting a piece of cardboard in the shape of the objects and drilling multiple holes in it. Then nail it to one of the holes on the wall and hang it freely. On the same nail, hang plumb. Using a pencil, draw the direction provided by the direction of the plumb’s end. This is where the object’s centre of gravity is placed. Replace the body in the other holes and repeat the procedure.
Difference Between a Centroid and a Centre of gravity
1.Definition of Gravity and Centroid
The centroid is the geometric centre of the thing, while the centre of gravity is the point where the total weight of the body acts. The centre of gravity, also known as the centre of mass, is the location where the body’s entire mass is concentrated. For every orientation of the body, this is where the gravitational force (weight) of the body acts. For objects of uniform density, the centroid is the centre of gravity.
2.Calculation of Gravity and Centroid
Because the mass (and weight) may not be evenly distributed throughout the item, calculating the centre of gravity is not an easy task. The centre of gravity can be computed using the formula cg × W=S × dw, where x is the distance from a reference line, dw is a weight increment, and W is the object’s total weight. Methods such as the plumb line method outlined above can be used to locate the centroid.
Things to Remember
The centre of gravity, also known as the centre of mass, is the location where the body’s entire mass is concentrated.
The equation W=s × dw can be used to compute the gravity centre.
- W – total weight of the object.
- X- distance from a reference line.
- dw-increment of weight.
The centroid is the place in any object’s geometric centre where the density is evenly distributed throughout the body.
The centroid is calculated using either the plumb line method or the median’s mean.
Both of these phrases have been used to define an object’s weight, density, and balance.
Conclusion
The operation of a resultant force with an intensity equal to the weight of the body, aimed at the body’s centre of gravity, can replace the gravitational forces of the body’s elementary pieces.
The gravitational centre is found at the junction of gravitational lines, and it is defined geometrically in the correct geometric bodies. This is correct if the density of the substance is the same throughout the body. In that scenario, the centroid of the body is the same as the centre of gravity.
The centroid of an object is the average position of all its points. It’s the point at which a form cut out could be mad
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






