Profile
Settings
Refer your friends
Sign out
Biot-Savart law, in physics, is the basic fundamental relationship between electricity and the magnetic field it produces, based on the study in 1820 by French scientists Jean-Baptiste Biot and Félix Savart.
In physics, especially electromagnetism, the Biot-Savart law is a mathematical equation that describes a magnetic field produced by a uniform electric current.
It associates the magnetic field with magnitude, direction, length, and proximity to electric current. Biot – Savart law is important in magnetostatics, playing a similar role that Coulomb’s law plays in electrostatics.
An electric current flowing through a conductor, or a moving electric charge, generates a magnetic field, or a region in a space around the conductor where the magnetic field may be experienced.
The amount of the magnetic field at a point in the surrounding area can be considered as the sum of all the contributions from each sub-element, or segment, of the current carrying conductor. Biot-Savart law states that the value of the magnetic field at a specific point in space from one short segment of the current conductor depends on each factor influencing the field.
Biot-Savart Law
According to Biot-Savart law, a segment of the current carrying conductor produces a magnetic field. That segment is referred to as the element of current and is a vector quantity.
In a statement, the Biot-savart’s law states that A point A’s magnetic intensity (dB) is directly proportional to the current I flowing through a small element (dl).
The Biot-Savart law states that at any point P due to the magnetic field dB due to element dl of a current-carrying is given by:
Biot- Savart Law in Vector Form
As we all know that the Magnetic Field is a vector Quantity hence Biot Savart Law can also be written in the form of vector.
Therefore if dl is the vector notation of current element in the direction of current flowing into the conductor and r is the vector of distant point so, Magnetic field at that point is determined by the help of Biot-Savart Law as:
Hence, this is the Biot-Savart Law in Vector Form.
Magnetic Field due to a Current Carrying Circular Loop
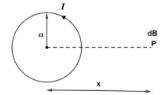
The magnetic field in the axis of circular loop is calculated using biot savart law. The mathematical formula to calculate the magnetic field at any particular point on the axis of the circular loop of radius a and current carrying I, at a point P far from it at a distance x is given by:
Application of Biot- Savart Law
There are following applications of Biot Savart Law:
- This law is used to evaluate the magnetic response at the molecular level.
- Biot savart law is used to assess the velocity in aerodynamic theory induced by the vertex line.
- This law is used to determine the magnetic fields in space due to any current carrying conductor.
- This Law is used to determine the force between two long and parallel current carry conductors.
- This law is also used to calculate the Magnetic field on the axis of a circular current loop.
Importance of Biot Savart Law
The importance of Biot Savart Law is mentioned below:
- This Biot Savart law is exactly similar to Coulomb’s law in electrostatics.
- Generally it is relevant for very small conductors that carry current.
- Biot Savart law is applicable for symmetrical current distribution.
Conclusion
In this article we have studied about Biot-Savart law and its importance. In physics, Generally Biot-Savart law is applied in a particular case by combining up the contributions to a magnetic field at a given point from the whole series of short current segments that constitute a specific conductor of any random shape.
For example, with a long wire carrying current, the value of the magnetic field at a point near it is just directly proportional to the value of the current and inversely proportional to the perpendicular distance from the wire to the given point.
