Profile
Settings
Refer your friends
Sign out
The tendency of any physical body to resist changes when rotated w.r.t a particular fixed line in the 3-D plane is the moment of inertia. This change can be evaluated using the centroid, where the overall impact of forces is zero. Thus, the tendency for different shapes to change physically can be assumed to depend on the centroid.
Centroid is the physical point present on the body, wherein the overall body concentrates its weight and balances itself to cancel out all kinds of forces. The centroid can be calculated depending upon the dimensions of the physical body. The size of the body does not affect the centroid, as it is the balancing point of the whole body. Thus, if we take a knife and place the body on its tip, the body is in equilibrium and balances itself without tumbling; the point is assumed to be the centroid of the given physical body.
Thus, the area moment of inertia can be evaluated for any physical body using the centroid.
Factors Affecting the Moment of Inertia
There can be infinite factors, the orientation being the major. If we have two physical bodies of the same area and shape, but the orientation is different, then the area moment of inertia would be different depending on the way the body is placed.
The other factor can be the shape of the physical body taken into consideration to evaluate the inertia. Now, the centroid changes for different bodies, and so does the area moment. For a body to be rectangular, the other to be circular, the centroid is different, even though we know that the centre is the centroid. By computation, the moment of inertia is unique for different bodies depending on their shape.
Some Basic Shapes
The area moment of inertia for some of the generic physical bodies or shapes is pre-defined based on their bending around the centroid:
Rectangle
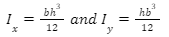
where b is the breadth and h is the height of the rectangle.
Also, the centroid is taken as the centre or the origin of the coordinate system. Area moment of inertia is defined w.r.t the x and y axes, respectively.
Circle
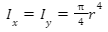
where r is the radius of the circle for which area moment of inertia is to be evaluated.
The area moment is defined over the centroid, which is the centre of the x and y axes.
Triangle
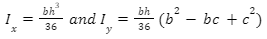
where b is the measurement of the triangle’s base, h is the triangle’s height from the base, and c is the distance between the top vertex to the nearest base vertex.
The area moment of inertia is evaluated when the centroid is the centre of the triangle and origin coincides with this point.
For asymmetrical body
The area moment of inertia is evaluated using the centroid as usual. For such bodies, evaluation of the centroid is the main computation. Thus, the x and the y coordinate is evaluated.
The first step is to divide and make sections to form the body from the basic and generic shapes. These shapes can be rectangles, circles and triangles, as we know the area moment of inertia and centroid for such generic bodies.
Now for each section, calculate the area using the dimensions and calculate the centroid as
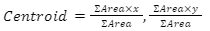
where x and y are the centroid coordinate for the respective section made from the whole body.
Now, for the overall area moment of inertia for the asymmetrical bodies, evaluate it using the formula given for the generic body and add the product of area and square of separation from the fixed line.
Application of Area Moment of Inertia
The area moment of inertia is used to evaluate the different mechanical designs and calculations for the bending resistance due to external forces or rotation. This can be used in buildings, the construction of bridges, and many more civil projects.
Conclusion
- The area moment of inertia for any physical body depends on the shape and the orientation.
- The area moment of inertia is evaluated w.r.t the x and y axes from the fixed line for bending effect.
- The different bodies have different centroids, and the area moment of inertia considers the point of centroid as the origin.
- The composite bodies can be segregated and sectioned into general bodies for simple calculation of area moment of inertia.
