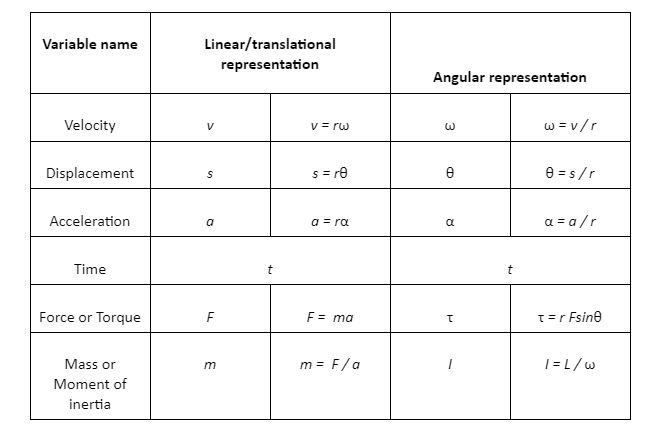
Understanding basic terms of translational and rotational motion

• Position: Position is any point in space. It could be on a linear or an angular surface. When it is on a circular surface, it is known as angular position.
• Displacement: When an object moves, the change in position from point A to point B is known as displacement.
• Linear Displacement: When an object moves, a change in position from point A to point B, where both points lie on a straight line, is known as linear displacement. That is when the angle does not change while travelling from point A to B.
• Angular Displacement: When an object moves, change in position from point A to point B, where both points lie at an angular distance. That is when the motion is circular or rotational while travelling from point A to B. Here, there is an angle change. This is known as angular displacement.
• Velocity: Velocity determines the speed of an object moving in a particular direction, also noting the time it takes to do so.
• Linear Velocity: The speed of an object moving in the forward direction is defined as linear velocity. Here the angle of movement remains linear. That is, there is no angular change. This is known as linear velocity.
• Angular Velocity: The speed of spinning movement of an object on a circular/angular surface is known as angular velocity. Here the motion is rotational, and, therefore, follows an angular spin instead of a linear movement.
• Acceleration: The change in velocity to time is noted as acceleration. Both direction and speed are important factors when talking about acceleration.
• Linear Acceleration: The change in velocity when divided by the change in time makes for linear acceleration.
• Angular Acceleration: The change in angular velocity when divided by the change in time makes for angular acceleration.
• Period: The time required to complete one cycle is known as a period. The unit used here is seconds.
• Frequency: The number of cycles occurring per second is known as frequency. It can also be termed as the reciprocal of the period. The unit used here is hertz.

 Angular displacement (θ)

The difference between the final angle of position and the initial angle of position is known as angular displacement. This displacement is noted on a circular or angular surface when there is a change in position from point A to point B, where both points lie at an angular distance from one another.

This is one of the most noted examples of angular variables and is represented by using the symbol ‘θ’.

θ = s / r

Here, ‘θ’ represents angular displacement,

‘s’ represents displacement,

and ‘r’ represents the radius of curvature.

The unit used for angular displacement is radian or degree.

 Angular velocity (ω)

An object’s angular velocity determines how fast or slow it spins on a circular surface. Here, the motion is rotational and follows an angular spin instead of a linear movement.

Another one of the three most noted examples of angular variables is that angular velocity is represented by the symbol ‘ω’.

ω = v / r

Here, ‘ω’ represents angular velocity,

‘v’ represents velocity,

and ‘r’ represents the radius of curvature.

 The unit used for angular velocity is radian per second or rad/s.

Note: While linear speed may change at different points, angular speed remains constant throughout the surface.

 Angular acceleration (α)

Angular acceleration can best be understood in terms of linear acceleration. When divided by the change in time, the change in velocity makes for linear acceleration. Similarly, when velocity in the above equation or definition is substituted by angular velocity, it results in angular acceleration. This gives us a new definition for angular acceleration. Therefore, angular acceleration is the change in angular velocity divided by the change in time.

Angular acceleration is the third and final one among the most noted examples of angular variables and is represented by using the symbol ‘α’.

 α = a / r

Here, ‘α’ represents angular acceleration,

‘a’ represents acceleration,

and ‘r’ represents the radius of curvature.

 The unit used for angular acceleration is radian per second squared or rad/s2.

 Conclusion

Angular velocity (ω), angular displacement (θ), angular acceleration (α), are three of the most noted angular variables examples and thus the foundational concepts of rotational motion. Other important terms as discussed above are position, period, frequency, torque, the moment of inertia.