Amplitude Phase

The phase is a sound wave’s one of the most important characteristics. The location of a point in a wave cycle that is periodic in nature is specified by the wave. For practical applications, what matters the most is the phase difference between different sound waves. The absolute values of the phases of the signals don’t actually matter. When different sound waves are added, the final output wave’s characteristics depend on the phase difference between the given two waves.

Constructive Interference

When two waves have the same frequency and are aligned perfectly with zero phase difference, then they are said to be in-phase. Adding these two in-phase waves together results in another wave whose amplitude is the sum of the amplitudes of the original waves. This whole process is known as Constructive Interference.

Destructive Interference

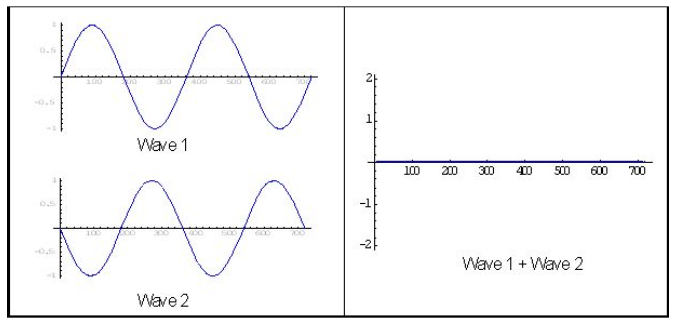
Let us consider two waves. They are in phase with each other and have the same frequencies. Let us call one of the waves A and the other wave B. Now, let us move wave A ahead of wave B by half cycle. This movement would be relative to wave B. This process results in such an arrangement that when wave A has maximum amplitude, wave B has minimum amplitude like wave 1 and wave 2 from the image below.

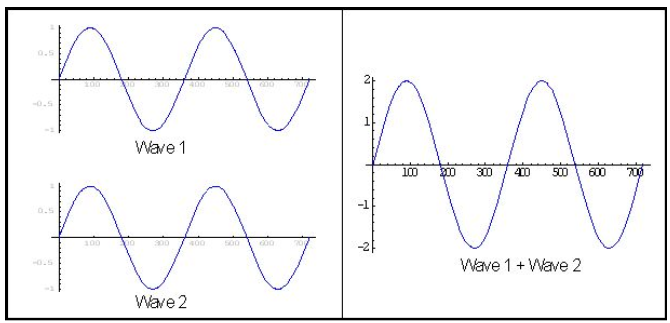
It is then said that these two waves are out of phase and cancel each other out.

This is the idea behind noise-cancelling headphones, which is called destructive interference in technical terms.

This phase difference between the two waves is usually expressed in an angle. It is not represented as a fraction of waveform. The phase difference is defined as an angle because the given wave, with a frequency, is essentially a sine wave.

If y(t) represents the waveform, then:

y(t) = A sin(2 π f t)

Where:

The amplitude is A.

The frequency is f in hertz or cycles/second.

Time is t in seconds.

In the above-given equation, the term (2πft) is an angle expressed in radians. We all know that the sine wave is periodic and has a waveform that repeats over time.

It helps to predict the locations on the given waveform accurately. And these locations are specified as angles in radians or degrees.

Amplitude

The maximum distance that a point on a vibrating wave or a body can move from its equilibrium position is called amplitude. For a periodic motion, the magnitude of the amplitude is half of the length of the path of the vibration. Consider a pendulum bob that is swinging back and forth. The amplitude of this pendulum bob would be half of the distance that this pendulum bob swings one way.

Waves amplitudes are proportional to the source amplitudes.

A transverse wave is like a plucked string wave. The amplitude is calculated by the maximum distance of a point on a string from its original position to a point when the string is not moving. While for a longitudinal wave, like a sound wave, the amplitude is calculated by the maximum distance of a point from its equilibrium position.

A wave is called damped when it’s constantly losing energy because the amplitude constantly keeps dropping.

Conclusion

It is important to remember that when the phase and other components of a wave are constant, the power of the wave is based on the amplitude. Higher amplitude implies higher power. If the waveform has lower peaks, then the amplitude will be lower. And hence the power provided that all other components of the waveform remain constant.