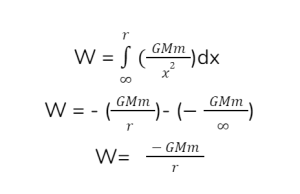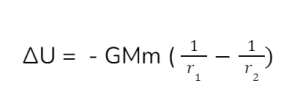There is a specific place of mass in space, where mass has to work against gravity to transport it, which we can get from the law of gravity. Let’s use gravity for the general term for potential energy. Gravitation is mainly used to reach zero over long distances, or to reach the zero point of gravitational potential energy at an unknown distance. Gravitational potential energy is also defined, Which will be discussed here.
The Gravitational Potential Energy Equation’s Derivation
Gravity is active when the mass approaches a planet, the nearby gravitational potential is negative. Gravitationists mainly define a “binding state” related to negative potential, which describes the state of a mass as it approaches a massive object, as well as to generate enough energy to release it. If we denote the gravitational potential energy of mass m, then its general form will be;
U = – GMm / r
G is the gravitational constant, M is the mass of the attractor, and r is the distance between their centres. This is the most common representation of gravitational potential energy to estimate the Earth’s gravity escape velocity.
The formula for gravitational potential energy is derived from the attempt to act on gravity by bringing the mass from infinity, where the potential energy is assigned the value zero.
U = – GMm/r
This expression can be used to calculate escape velocity, orbital energy and others. However, for objects close to the Earth’s surface, the acceleration due to gravity, g, can be assumed to be almost constant, and the formula for potential energy with respect to the Earth’s surface becomes.
U = mgh
where h is the height above the surface and g is the acceleration of gravity at the surface.
Consider the following scenario: A source mass ‘M’ is placed at a location along the x-axis, and a test mass ‘m’ is originally at infinity. It is given by a modest amount of work done in transporting it through a very small distance (dx) without acceleration.
Fdx = dw
F is an attracting force, and the displacement is in the direction of the negative x-axis, therefore F and dx are in the same direction. Then,
dW = (GMm/x2)dx
Integrate
Because the work done is stored as potential energy U, gravitational potential energy at a distance ‘r’ from the source mass is calculated as follows:
U = – GMm/r
If a test mass moves from one place inside the gravitational field to another point within the same gravitational field as the source mass, the potential energy of the test mass changes as follows:
Related some question
The gravitational potential is -5.12 × 107 J/kg and the acceleration due to gravity is 6.4 m/s2 at a location above the earth’s surface. Calculate the height of this point above the earth’s surface, assuming the earth’s mean radius is 6400 km.
Solution
Let r be the distance between the provided point and the earth’s centre. Then,
Gravitational potential = -GM/r = -5.12 × 107 J/kg …… (1)
and acceleration due to gravity,
g = GM/r2 = 6.4 m/s2 …… (2)
When we divide (1) by (2), we get
r = 5.12 × 107/6.4 = 8 × 106 m = 8000km
As a result, the height of the point above the earth’s surface = r – R = 8000 – 6400 = 1600 km
Calculate the gravitational potential energy of a body with a mass of 20 kilogrammes and a height of 30 metres above the earth.
Solution- If given mass , m = 20 kilogram
Height = 30 metre
We know that , Gravitational potential energy , U = mgh
Put g = 9.8 m/s2
U = 20 × 30 × 9.8
= 5880 J
If the earth’s mass is 3.24 × 1020 kilograms and the sun’s mass is 2.4×1025 kilogrammes, and the earth is 120 million kilometres away from the sun, Calculate the earth’s gravitational potential energy.
Solution – Given us, mass of the earth, m = 3.24 × 1020
sun’s mass is M = 2.4×1025
We know that , Gravitational potential energy , U = – GMm/r
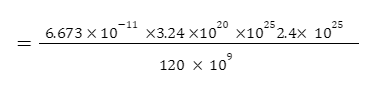
= 4.32 × 1025 J
Conclusion
The term “potential energy” refers to the energy contained in an object. Elastic potential, chemical potential, and gravitational potential energy are all examples of potential energy. For example, elastic potential energy is the energy contained in a spring. The energy contained in chemical molecules is called chemical potential.
The energy contained in an object due to its height is called gravitational potential energy (GPE). The value of GPE is proportional to and affected by height. Therefore, if the height of an object is doubled, its gravitational potential energy also doubles. If the height is tripled, the GPE value will also triple, and so on.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out