
Be a part of Last Mile Program for JEE 2024
Acceleration due to gravity is the acceleration an object receives due to gravity. SI unit of acceleration due to gravity (gravitational acceleration) is . Gravitational acceleration has both magnitude as well as direction. It is therefore a vector quantity.
We represent the gravitational acceleration with the symbol g. Normal value of acceleration due to gravity on the surface of the earth at sea level is 9.8 m². The acceleration due to gravity formula is based on Newton’s second law of motion and Newton’s law of universal gravitation.
![]() Here,
f = force
g = acceleration due to gravity
m = mass
From universal law of gravitation
Here,
f = force
g = acceleration due to gravity
m = mass
From universal law of gravitation
![]() Here,
f = force between two bodies
G = universal gravitational constant
Here,
f = force between two bodies
G = universal gravitational constant ![]() M = mass of earth
m = mass of body
r = radius of earth
h = height of body from the surface of earth
Now, from both equations, we get the acceleration due to gravity formula.
M = mass of earth
m = mass of body
r = radius of earth
h = height of body from the surface of earth
Now, from both equations, we get the acceleration due to gravity formula.
![]() Therefore,
Therefore,
![]()
![]() g = acceleration due to gravity
h = height from earth surface
R = radius of earth
= acceleration due to gravity at height h
We know that, gravitational force exerted on a body of mass m is given as
g = acceleration due to gravity
h = height from earth surface
R = radius of earth
= acceleration due to gravity at height h
We know that, gravitational force exerted on a body of mass m is given as
![]() Here,
f = force between two bodies
G = universal gravitational constant ( )
M = mass of earth
m = mass of body
r = radius of earth
At a height of h,
Here,
f = force between two bodies
G = universal gravitational constant ( )
M = mass of earth
m = mass of body
r = radius of earth
At a height of h,
![]() Therefore
Therefore ![]() ————- (1)
Now, on the surface of earth, acceleration due to gravity is given as
————- (1)
Now, on the surface of earth, acceleration due to gravity is given as
![]() ————- (2)
Divide equation 2 and 3 then we get
————- (2)
Divide equation 2 and 3 then we get
![]() From the formula, we conclude that the value of acceleration due to gravity decreases when height of an object increases. Therefore, the value of acceleration due to gravity is zero at the distance of infinity from the earth.
From the formula, we conclude that the value of acceleration due to gravity decreases when height of an object increases. Therefore, the value of acceleration due to gravity is zero at the distance of infinity from the earth.
![]() Here,
= acceleration due to gravity at depth d
g = acceleration due to gravity
R = radius of earth
d = distance below the earth
we know the value of acceleration due to gravity on the surface of earth is determined by
Here,
= acceleration due to gravity at depth d
g = acceleration due to gravity
R = radius of earth
d = distance below the earth
we know the value of acceleration due to gravity on the surface of earth is determined by
![]() ———— (1)
Value of acceleration due to gravity at a distance d below the surface of earth is
———— (1)
Value of acceleration due to gravity at a distance d below the surface of earth is
![]() ————- (2)
Divide equation 1 and 2 then we get
————- (2)
Divide equation 1 and 2 then we get
![]() If d = 0 then, gd=g
If d = R then, gd=0
If d = 0 then, gd=g
If d = R then, gd=0
![]() The force by the earth attracts an object towards its centre
Principle of equivalence states that the inertial mass and gravitational mass are similar.
The value of acceleration due to gravity is inversely proportional to the height above the earth’s surface, so it gets reduced with increasing height.
acceleration due to gravity when height is given, is determined by
The force by the earth attracts an object towards its centre
Principle of equivalence states that the inertial mass and gravitational mass are similar.
The value of acceleration due to gravity is inversely proportional to the height above the earth’s surface, so it gets reduced with increasing height.
acceleration due to gravity when height is given, is determined by
![]() The value of Acceleration Due to Gravity with depth lies just below the surface of the earth, so it increases with depth, but becomes zero at the centre of the earth.
Acceleration due to gravity when depth d is given, is determined by
Acceleration due to gravity is represented by g.
The value of Acceleration Due to Gravity with depth lies just below the surface of the earth, so it increases with depth, but becomes zero at the centre of the earth.
Acceleration due to gravity when depth d is given, is determined by
Acceleration due to gravity is represented by g.
![]() ms-2 the SI unit of gravitational acceleration
ms-2 the SI unit of gravitational acceleration
Acceleration due to gravity is equal to 9.806m/s2
Acceleration due to Gravity Formula
As we know that the force which acts on a body due to gravity is given as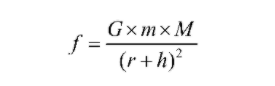 Here,
f = force between two bodies
G = universal gravitational constant
Here,
f = force between two bodies
G = universal gravitational constant 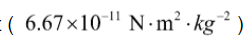 M = mass of earth
m = mass of body
r = radius of earth
h = height of body from the surface of earth
Now, from both equations, we get the acceleration due to gravity formula.
M = mass of earth
m = mass of body
r = radius of earth
h = height of body from the surface of earth
Now, from both equations, we get the acceleration due to gravity formula.
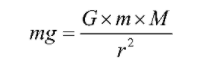 Therefore,
Therefore,
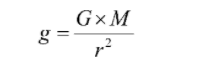
Gravity
The force by the earth attracts an object towards its centre Principle of equivalence states that the inertial mass and gravitational mass are similar.Variation of Acceleration Due to Gravity
Variation of Acceleration Due to Gravity with height
The value of acceleration due to gravity is inversely proportional to the height above the earth’s surface, so it gets reduced with increasing height. The variation of acceleration due to gravity with height is determined by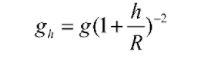 g = acceleration due to gravity
h = height from earth surface
R = radius of earth
= acceleration due to gravity at height h
We know that, gravitational force exerted on a body of mass m is given as
g = acceleration due to gravity
h = height from earth surface
R = radius of earth
= acceleration due to gravity at height h
We know that, gravitational force exerted on a body of mass m is given as
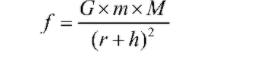 Here,
f = force between two bodies
G = universal gravitational constant ( )
M = mass of earth
m = mass of body
r = radius of earth
At a height of h,
Here,
f = force between two bodies
G = universal gravitational constant ( )
M = mass of earth
m = mass of body
r = radius of earth
At a height of h,
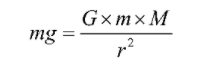 Therefore
Therefore 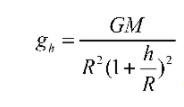 ————- (1)
Now, on the surface of earth, acceleration due to gravity is given as
————- (1)
Now, on the surface of earth, acceleration due to gravity is given as
 ————- (2)
Divide equation 2 and 3 then we get
————- (2)
Divide equation 2 and 3 then we get
 From the formula, we conclude that the value of acceleration due to gravity decreases when height of an object increases. Therefore, the value of acceleration due to gravity is zero at the distance of infinity from the earth.
From the formula, we conclude that the value of acceleration due to gravity decreases when height of an object increases. Therefore, the value of acceleration due to gravity is zero at the distance of infinity from the earth.
Variation of Acceleration Due to Gravity with the given depth
The value of Acceleration Due to Gravity with depth lies just below the surface of the earth, so it increases with depth, but becomes zero at the center of the earth. The acceleration due to gravity when depth is given, is determined by Here,
= acceleration due to gravity at depth d
g = acceleration due to gravity
R = radius of earth
d = distance below the earth
we know the value of acceleration due to gravity on the surface of earth is determined by
Here,
= acceleration due to gravity at depth d
g = acceleration due to gravity
R = radius of earth
d = distance below the earth
we know the value of acceleration due to gravity on the surface of earth is determined by
 ———— (1)
Value of acceleration due to gravity at a distance d below the surface of earth is
———— (1)
Value of acceleration due to gravity at a distance d below the surface of earth is
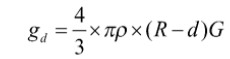 ————- (2)
Divide equation 1 and 2 then we get
————- (2)
Divide equation 1 and 2 then we get
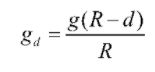 If d = 0 then, gd=g
If d = R then, gd=0
If d = 0 then, gd=g
If d = R then, gd=0
Conclusion
Acceleration due to gravity is the acceleration an object receives due to gravity. The acceleration due to gravity formula.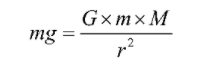 The force by the earth attracts an object towards its centre
Principle of equivalence states that the inertial mass and gravitational mass are similar.
The value of acceleration due to gravity is inversely proportional to the height above the earth’s surface, so it gets reduced with increasing height.
acceleration due to gravity when height is given, is determined by
The force by the earth attracts an object towards its centre
Principle of equivalence states that the inertial mass and gravitational mass are similar.
The value of acceleration due to gravity is inversely proportional to the height above the earth’s surface, so it gets reduced with increasing height.
acceleration due to gravity when height is given, is determined by
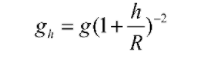 The value of Acceleration Due to Gravity with depth lies just below the surface of the earth, so it increases with depth, but becomes zero at the centre of the earth.
Acceleration due to gravity when depth d is given, is determined by
Acceleration due to gravity is represented by g.
The value of Acceleration Due to Gravity with depth lies just below the surface of the earth, so it increases with depth, but becomes zero at the centre of the earth.
Acceleration due to gravity when depth d is given, is determined by
Acceleration due to gravity is represented by g.
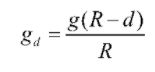 ms-2 the SI unit of gravitational acceleration
ms-2 the SI unit of gravitational acceleration Acceleration due to gravity is equal to 9.806m/s2
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out





