What is the Relation between two Circles?

A circle is a plane figure bounded by a single curved line, and all straight lines drawn from any point within the circle to the bounding line are equal. A Circle is a figure having many components. The main components to define the circle is the circumference, radius, diameter and the center of the circle.

What exactly is radius?

The radius is a line segment that connects the center of a circle or sphere to its perimeter or boundary in geometry. It is generally abbreviated as ‘r’. The plural of radius is “radii,” which is used when discussing multiple radiuses at once. The diameter is the longest line segment in a circle or sphere connecting any points on the opposite side of the center, while the radius is half the diameter’s length. It can be written as d/2, where d is the circle or sphere’s diameter.

Let us first have a brief idea about the different parts of the circle-

• Secant: It is the line that intersects the circle at two unique places.  
• Tangent :A line that touches the circle exactly at one point. The tangent to the circle is a line that touches the circle at a single point and stretches indefinitely.
• Chord: A chord of the circle is a line segment that connects two places on the circumference of a circle. Any number of chords can be found in a circle. A circle’s diameter is its largest chord.
• Segment: A segment of the circle is a portion of a circle circumscribed by a chord and an arc.
• Arc: An arc is a part or a portion of the circumference of a circle.
• Sector: A circle’s sector is the area enclosed by two radii and a circle’s arc. 

When we consider a circle, they will have different radius, diameter and the center. Let us assume that the two circles have radius r1 and r2  respectively. 

Two circles in the same plane

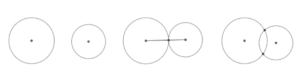
Two circles when lying on the same plane they may intersect, circumscribe, separate, inscribe and include by following different conditions which are as follows. Let us consider two circles with radius r1 and r2. Let the distance separating their center be d.

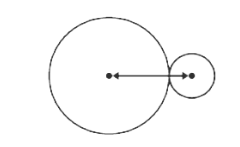
• Two circles will touch each other if the distance between their centers is equal to the sum of their radii, or the difference between their radii. They may be indicated as circles touching externally and internally. Two circles will touch if the distance between their centers ‘d’ is equal to the sum of their radii, or the difference between their radii. Mathematically we can represent this as,

d = r1 – r2  or  d = r1 + r2

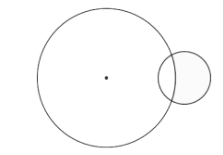
1. When the distance between the two circle centers is equal to the sum of the two radii, d = r1 + r2, it can be seen that they have only one intersection point between them. The two circles will have a common tangent.

1. When the distance between their centers is equal to the difference of the two radii, d = r1 – r2 , it can be seen that they share only one point between them. The two circles will have a common tangent. One of the circles is inside the other circle. Mathematically,

• Two circles will intersect at two points if the difference between their radius is smaller than the distance separating their centers. This can also be defined if the sum of their radius is greater than that of the distance separating their centers which is defined by ‘d’. The two coplanar circles i.e.lying on the same plane will have two points of intersection. Mathematically it can be represented as 

r1 − r2 < d < r1 + r2

• Two circles will also intersect at two points if the radius of the big circle is equal to the distance separating their centers. This can be understood by the following diagram. This can be defined mathematically as,

d = r1

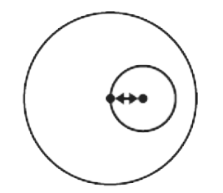
• One of the circles lies in the other when the distance between the center is equal to the  radius of the small circle. This can be understood by the following diagram. Mathematically,

d = r2

• If two circles have a common center irrespective of their radius, they are said to be concentric circles. They are circles having a common center. The region between two concentric circles of different radii is called an annulus. Any two circles can be made concentric by inversion by picking the inversion center as one of the limiting points. This can be defined mathematically as,

d = 0

Conclusion

When two circles are coplanar i.e. lying in the same plane and of different radius and separated by a distance from the center of the one to the other, they may intersect at zero, one or two points which we have learnt in the above article. The circles may circumscribe, intersect, circumscribe, separate, inscribe and include by following different conditions which we have read in the article. The total difference of the different cases totally depends on the radius of the two circles and the distance separating their centers.