Before directly going to the geometric significance of differential equations, let us have a brief discussion on differential equations. A differential equation incorporates one or more than one function along with their derivatives. The derivatives of a function define the rate of change of the function at a given point in time.
Derivatives, of which a differential equation may contain either partial or conventional derivatives, are present in the equation. A differential equation is a mathematical expression that shows how these functions and their derivatives combine to form an equation.The derivative stands for a rate of change, and the equation itself describes the relationship between the two quantities.
The highest order derivative determines the order of the equation. The power to which a differential equation raises its highest order derivative can be used to characterize it. This is referred to as the equation’s degree.
First Order Differential Equation and Geometric Significance
An equation of the form dy/dx =f (x,y) is used to describe a first-order differential equation. This following equation has two independent variables, x and y.the function f(x,y) can be defined by a region in the xy-plane. Due to the fact that it possesses just the first derivative, dy/dx, the resulting equation is of the first order, and there are no higher-order derivatives. The representation of first-order reaction is,
(d/dx)y = y’ = f (x,y)
It is possible to graph the solutions to differential equations in a number of different ways, each of which offers a unique perspective on the structure of the solutions. For first order differential equations there may be two possibilities of graphical representation. They are-
I. The Exponential Growth Model is the first type. Within the first order differential equation, there are many functions or systems that stretch at an exponential rate. For example,
dy/dt = ky
The k in the above equation is the growth rate constant. The graph of the above equation is as follows.
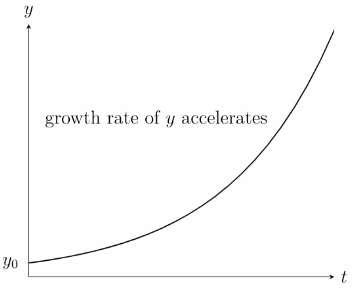
Population growth curve is one of exponential growth
II. The second type is the logistic growth model, which is based on the idea that as a number grows, other things will affect it and slow it down until it gets close to a certain maximum size.
For instance, if a population grows, there may be insufficient food or people may become ill. This sums up that growth of the population until it reaches a size that is sustainable. If you replace k in the simple model with r(My), the growth rate goes down as y goes up, and the maximum population size that can be maintained is M. This most it can hold is called its carrying capacity. So the basic model can be written as,
dy/dt = ry(M−y)
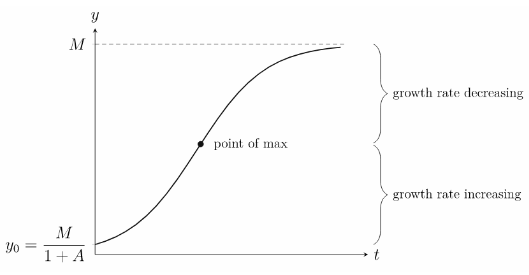
Geometrical Interpretation−Differential Equation
Since a differential equation of the first order and the first degree comprises two variables, an independent variable, say x, and a dependent variable, say y. it is possible to express it in any one of the following forms.
dy/ dx = f(x, y)
or
f (x, y) = 0
or
f(x, y) dx + g(x, y)dy = 0
Where f(x, y) and g(x, y) are functions of x and y. The general from-
f(x, y, dy/dx) = 0 …..(i)
We know that the direction of a curve in the direction of the tangent in Cartesian rectangular coordinates at any point is given by dy/dx, so the equation in (i) can be thought of as a relationship between the coordinates of a point and the slope of the tangent, dy/dx, to the integral curve at that point.The differential equation can be obtained by (i) which must be solved by identifying the curves along which the tangent at each point is parallel to the field’s direction.
Finding the locus of a differential equation is done by adding up all of the different curves that can be obtained from the general solution. The general solution of the equation of first order consists of a single arbitrary constant, and the locus of the equation can be defined as a single infinite number of curves.
Conclusion
Differential equations have a very important geometric significance and graphical interpretation in science and mathematics. When it comes to the mathematical modeling of physical systems, differential equations play a very significant role. The exponential growth pattern is seen in a wide variety of functions and systems that contain a first-order differential equation. In biology and economics and many other subjects, differential equations are used to understand the behavior of complex systems.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out