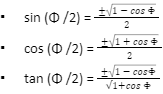Watch Free Classes

Trigonometric identities are equalities using trigonometric functions that hold true for any value of the variables involved, hence defining both sides of the equality. The Sin, tan, and cos are the three main trigonometric ratios. The reciprocals of sin, cos, and tan are represented by the three additional trigonometric ratios sec, cosec, and cot in trigonometry.

Trigonometric identities

The Trigonometric identities can be defined as the equations that is true for all the value of the variable in the domain and relate to various trigonometric functions. An identity is simply an equation that holds true for all conceivable values of the variable(s) contained inside it.

Trigonometric identities are equations that relate to various trigonometric functions and are true for every variable value in the domain. An identity is essentially an equation that holds true for all values of the variable(s) included in it.

Type of Trigonometric Identities

There are following trigonometric identities in mathematics, and they are

Basic Identities: The Basic identities of trigonometry are in the following; 

  • Sin Φ = perpendicular/hypoteneous

  • Cos Φ = Base/hypoteneous

  • Tan Φ = hypoteneous/base

  • Cot Φ = base/hypoteneous

  • Sec Φ = hypoteneous/base

  • cosec Φ = hypotenues/perpendicular

Pythagorean Identities: some of the Pythagorean identities are

  • cos2 Φ + sin2 Φ = 1

  • sec2 Φ = 1 + tan2 Φ 

  • cosec2 Φ  = 1 + cot2 Φ 

Negative Angle Identities

  • Sin (-Φ) = – Sin Φ

  • Cos (-Φ) = Cos Φ

  • Tan (-Φ) = – Tan Φ

  • Cot (-Φ) = – Cot Φ

  • Sec (-Φ) = Sec Φ

  • Cosec (-Φ) = -Cosec Φ

Double-Angle Identities

  • sin 2 Φ = 2 sin Φ cos Φ

  • cos 2 Φ = cos2 Φ – sin2 Φ = 2 cos2 Φ – 1 = 1 – 2sin2 Φ

  • tan 2 Φ = (2tan Φ) / (1 –tan2 Φ  )

Complementary and supplementary Trigonometric Identities

  • sin (90°- Φ) = cos Φ

  • cos (90°- Φ) = sin Φ

  • cosec (90°- Φ) = sec Φ

  • sec (90°- Φ) = cosec Φ

  • tan (90°- Φ) = cot Φ

  • cot (90°- Φ) = tan Φ

  • sin (180°- Φ) = sin Φ

  • cos (180°- Φ) = -cos Φ

  • cosec (180°- Φ) = cosec Φ

  • sec (180°- Φ) = -sec Φ

  • tan (180°- Φ) = -tan Φ

  • cot (180°- Φ) = -cot Φ

Half-Angle Identities

Product Identities

  • Sin Φ. Sin β = [Cos (Φ – β) – Cos (Φ + β)]/ 2

  • Sin Φ. Cos β = [Sin (Φ + β) – Sin (Φ – β)]/ 2

  • Cos Φ. Cos β = [Cos (Φ + β) – Cos (Φ – β)]/ 2

Sum and Difference Trigonometric Identities

The sum and difference trigonometric identities are in the following; 

  • sin ( Φ + β) = sin Φ cos β + cos Φ sin β

  • sin (Φ – β) = sin Φ cos β – cos Φ sin β

  • cos (Φ + β) = cos Φ cos β – sin Φ sin β

  • cos (Φ – β) = cos Φ cos β + sin Φ sin β

  • tan (Φ + β) = (tan Φ + tan β) / (1 – tan Φ tan β)

  • tan (Φ – β) = (tan Φ – tan β)/ (1 + tan Φ tan β)

Significance of Trigonometric Identities

The significance of Trigonometric Identities are in the following;

  • Archaeologists uncover a variety of devices used by the civilization; trigonometry might help them with these digs. It may also be used to calculate the separation between subterranean water systems.

  • It can be used in oceanography also to calculate the height of tides.

  • The sine and cosine functions are crucial to periodic function theory, which describes sound and light waves.

  • Calculus consists of Trigonometry and Algebra.

  • Trigonometry may be used to roof a home, make the roof slanted (in the case of single-family bungalows), and determine the height of a building’s roof, among other things.

  • It is used in the marine and aviation sectors.

  • It can be used in cartography (creation of maps).

  • Trigonometry is used in satellite systems as well.

  • In computer imaging, trigonometry is critical. It is frequently employed in computer graphics to create dense and complicated pictures. The process used to create such precise images is known as triangulation. This approach employs a number of trigonometric concepts.

Conclusion 

Trigonometry may not have many everyday applications, but it does make working with triangles easier. It’s a useful supplement to geometry and actual measurements, and as such, it’s worth learning the fundamentals even if you never want to go any further.