Types of Sequences

In mathematics, a sequence is a list of elements (most of the time, numbers) in which the order of the elements is important. The parts of this composition are organised in a certain way. In real life, we come across sequences in a variety of settings. The numbers of houses in a row, the amount of money earned in successive years (either by a predetermined amount or by a certain percentage), the page numbers of a book, and so on are all examples of sequences. 

Sequences: 

The term “sequence” refers to an enumerated collection of things in which repeats are permitted and the order of the objects is important. It is similar to a set in that it contains members (also called elements, or terms). The length of a series is defined as the number of elements in the sequence (which may be infinite). A sequence differs from a set in that the same items can appear more than once in a sequence at different points, and unlike a sequence, the order of the components is important. On a formal level, the sequence can be described as a function that maps natural numbers (the positions of individual elements in a sequence) to elements at each point in the series. The concept of a sequence can be extended to include the concept of an indexed family, which is defined as a function from an index set that may or may not be composed entirely of numbers to another set of elements. 

Order of the sequence: 

The order of a sequence can be either ascending or descending, depending on the context of the sequence. 

Ascending order: 

If the elements of the sequence are presented in increasing order, then the sequence’s ascending order is indicated.

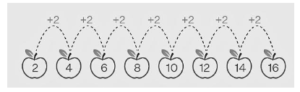
The preceding sequence is in ascending order because the items in it are “growing” by a factor of 2. 

Descending order: 

Similarly, if the elements of the sequence are arranged in decreasing order, the sequence’s order is described as declining. 

The preceding sequence is in descending order because the terms in it are “decreasing” by four points. 

Finite and infinite sequences: 

Finite sequence: 

A finite sequence is a series that has a finite number of terms in each iteration. If a ball bounces a certain number of times before coming to a complete stop, the sequence is called a finite sequence. 

Infinite sequence: 

It is referred to as an endless sequence when a sequence has an infinite number of terms. Consider the following example: a sequence of natural numbers (for example, 1, 2, 3, 4, and so on) generates an infinite sequence.

Special sequences in maths: 

In mathematics, there are several particular sequences, such as the arithmetic sequence and geometric sequence, as well as the Fibonacci series and harmonic sequence, the triangular number sequence, the square number sequence, and the cube number sequence Aside from these, sequences that follow a different pattern can also be found in nature. Example: The sequence 2, 9, 28, 65,… is a sequence in which the numbers can be written as 1³ + 1, 2³+1, 3³+1, 4³+1, and so on, and this sequence does not belong to any of the subsequent sequences. 

Arithmetic sequence: 

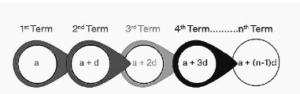
As the name implies, an arithmetic sequence is a sequence of numbers in which each successive term is the sum of the term before it and a fixed number. An arithmetic sequence can be represented as The term for this set value is “common difference.” It is possible to write the terms of the arithmetic sequence in the following ways: a, a+d, a+2d, etc. 

Quadratic sequence: 

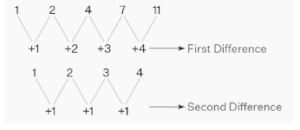
In our last discussion, we learned that if the differences (also known as initial differences) between every two succeeding terms are equal, the sequence is referred to as an arithmetic sequence (which is also known as a linear sequence). The sequence is characterised as a quadratic sequence if, however, the initial differences are not identical and, instead, the second differences are identical. 

Example: Because their second differences are the same, the sequence 1, 2, 4, 7, 11,… is a quadratic sequence. Take a look at the illustration on the left.

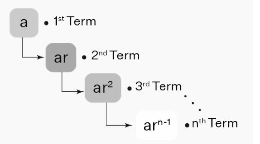
Geometric sequence: 

Any sequence in which every term bears a constant ratio to its preceding term is known as a geometric sequence. Known as the “common ratio,” this proportion is used in many applications. All of the words in the geometric series are of type a, ar, ar²,…..

Harmonic sequence: 

A harmonic sequence is a series that is formed by taking the reciprocal of the components of an arithmetic sequence and adding them together. 

Example: Natural numbers are arithmetic sequences, as we all know. As a result, if we take the reciprocals of each term, we get 1, 1/2, 1/3,…, which is a harmonic sequence, just as their reciprocals 1, 2, 3,… form an arithmetic sequence. 

Rules of sequences: 

When dealing with a series (whether geometric or mathematical), we can often divide it into two sorts of rules.

• When a phrase is represented in terms of its prior term, there is an implicit rule.
• A rule that is explicit in that any term may be obtained by utilising a general formula. 

Points to remember: 

• The common difference between each subsequent phrase in an arithmetic sequence is produced by adding the preceding term’s common difference to the following term.
• In a geometric sequence, each succeeding term is created by multiplying the common ratio of its preceding phrase by the common ratio of its preceding term and so on.
• Arithmetic sequences are formed by taking the reciprocal of each phrase in a harmonic sequence. 

Conclusion: 

Sequences can be used in a variety of situations. The method of listing the first few words and then looking for patterns that will assist in obtaining the general term is effective when solving problems requiring sequences. When the general term is discovered, it is possible to find any term in the series without having to write down all of the terms that came before it.