This discussion centres on the procedure for determining the highest and lowest possible values of a function within a particular domain, as suggested by the topic’s name. It is applicable to almost every area of work as well as every field of study. Let’s learn more about the highest and lowest points associated with this subject area.

Applications of Maxima Minima

The following is a list of some applications that are used on a daily basis:

• An engineer will tell you that the maximum and minimum values of a function can be used to determine the boundaries of the function when it is applied in the real world. For example, if you can find a suitable function for the speed of a train, then determining the maximum possible speed of the train can help you choose the materials that would be strong enough to withstand the pressure caused by such high speeds, and these materials can be used to manufacture the brakes and the rails, among other things, so that the train runs smoothly. If you can’t find a suitable function for the speed of a train, then you won’t be able to determine the maximum possible speed of the
• To an economist, the maximum and minimum values of the total profit function can be used to get an idea of the limits that the company must put on the salaries of the employees in order to keep from going into loss. This is done so that the company does not go into loss.
• To a doctor – The maximum and minimum values of the function that describes the total thyroid level in the bloodstream can be used by the doctor to determine the dosage that needs to be prescribed to each individual patient in order to bring their thyroid levels back to normal.

The various Maxima and Minima Types

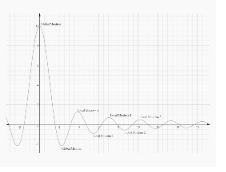
An extreme value of the function is also referred to as an extremum, which can refer to either the maxima or the minima. Let us assume that we have a function with the definition y = f(x) that is defined on a known domain of x. The extremum can be referred to as either a “local” or a “global” extremum, and this designation is determined by the interval of x on which the function reaches its maximum value. Let’s get a better understanding of it using maxima as an example.

Local Maxima

A point is said to be a Local Maxima of a function when there may be some other point in the domain of the function for which the value of the function is greater than the value of the local maxima, but such a point does not exist in the vicinity or neighbourhood of the local maxima. In other words, a point is said to be a Local Maxima of a function when it is possible that there may be some other point in the domain of the function for which the value of the function is greater It is also possible to interpret it as a maximum value in relation to the points that are located nearby.

Global Maxima

When there is no other point in the domain of the function for which the value of the function is greater than the value of the global maxima, a point is said to be the global maxima of the function. A point is known as a Global Maxima of a function when this condition is met. Different kinds of global maxima include:

It is possible for global maxima to fulfil all of the requirements of local maxima. It is also possible to interpret it as the Local Maxima with the highest possible value in this scenario.

The alternative is that the global maxima of an increasing function could be the endpoint in its domain, since this point would obviously have the highest value. In this particular instance, the function does not have a local maximum.

In a similar vein, both the local and the global minima are determinable. Take a look at the graph that follows to learn more about the various kinds of maxima and minima.

Conclusion

An extreme value of the function is also referred to as an extremum, which can refer to either the maxima or the minima.A point is said to be a Local Maxima of a function when there may be some other point in the domain of the function for which the value of the function is greater than the value of the local maxima, but such a point does not exist in the vicinity or neighbourhood of the local maxima.When there is no other point in the domain of the function for which the value of the function is greater than the value of the global maxima, a point is said to be the global maxima of the function.