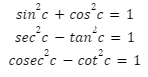TRIGONOMETRIC IDENTITIES

As we know that an identity is an equation that is true for all variables present in that equation and trigonometry is the study of the relation between the angle and the sides of a triangle. When we combine both the words trigonometry and identities, we get trigonometry identities which means the equations involving the trigonometric ratios and that satisfies for all the values of the angles involved in the equation.

Trigonometric identities are equalities using trigonometric functions that hold true for any value of the variables involved, hence defining both sides of the equality. We will look at trigonometric identities in this mini lesson. Sin, cos, and tan are the three main trigonometric ratios. The reciprocals of sin, cos, and tan are represented by the three other trigonometric ratios sec, cosec, and cot in trigonometry.

Trigonometric identities are used to solve geometric, trigonometric, and other math issues. They are equations that always hold true.

The six trigonometric ratios serve as the foundation for all trigonometric identities. Sine, cosine, tangent, cosecant, secant, and cotangent are the mathematical terms for sine, cosine, tangent, cosecant, secant, and cotangent. The sides of the right triangle, such as the adjacent, opposing, and hypotenuse sides, are used to define all these trigonometric ratios. The 6 trigonometric ratios which are the source of all fundamental trigonometric identities.

To solve the issues, all trigonometric identities are used. Pythagorean identities, reciprocal identities, sum and difference identities, double angle and half-angle identities are the most important trigonometric identities. We’ll need to use the sine and cosine rules for non-right-angled triangles.

Trigonometric identities are equations that relate to various trigonometric functions and are true for any variable value in the domain. An identity is essentially an equation that holds true for all possible values of the variable(s) in it.

Some algebraic identities are, for example:

• (a + b)2 = a2 + 2ab + b2

• (a – b)2 = a2 – 2ab+ b2

• (a + b)(a-b)= a2 – b2

The algebraic identities only apply to the variables, but the trigonometric identities pertain to the six trigonometric functions sine (Sin), cosine (Cos), tangent (tan), cosecant (Cosec), secant (sec), and cotangent (Cot).

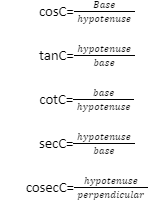
TRIGONOMETRIC RATIOS

RECIPROCAL IDENTITIES OF TRIGONOMETRIC

SinC = 1/CosecC a Cosec C = 1/Sin C

Cos C = 1/Sec C or SecC = 1/Cos C

Tan C= 1/Cot C or Cot C= 1/Tan C

Trigonometric Pythagorean Identities

In trigonometry, there are three Pythagorean trigonometric identities based on the right-triangle theorem or Pythagoras theorem.

Ratio trigonometric identities

tanC = SinC/ CosC                   

and           

cotC=cosC / sinC

Identities of Opposing Angles in Trigonometry

The following are some examples of opposite angle trigonometric identities:

Sin (-C) = – Sin C

Cos (-C) = Cos C

Tan (-C) = – Tan C

Cot (-C) = – Cot C

Sec (-C) = Sec C

Cosec (-C) = -Cosec C

Trigonometric Identities of Complementary Angles

The following are some examples of complementary angle trigonometric identities:

Sin (90° – C) = Cos C

Cos (90° – C) = Sin C

Tan (90° – C) = Cot C

Cot ( 90° – C) = Tan C

Sec (90° – C) = Cosec C

Cosec (90° – C) = Sec C

Trigonometric Identities of Supplementary Angles

The following are some examples of Supplementary angle trigonometric identities:

Sin (180° – C) = Sin C

Cos (180° – C) = -Cos C

Tan (180 °– C) = -Tan C

Cot ( 180°– C) = -Cot C

Sec (180° – C) = -Sec C

Cosec (180° – C) = Cosec C

Sum and Difference of Angles Trigonometric Identities

Assuming two angles, A and B, the trigonometric identities of sum and difference of angles are as follows:

sin(α+β)=sin α.cos β+cos α.sin β

sin(α–β)=sin α.cos β–cos α.sin β

cos(α+β)=cos α.cos β–sin α.sin β

cos(α–β)=cos α.cos β+sin α.sin β

Trigonometric Identities of double the Angle

The following are the trigonometric identities of double the angles:

sin 2C = 2 sin C cos C

cos 2C = cos2c– sin2c= 2 cos2c– 1 = 1 – 2sin2c

tan 2C = (2tanC)/(1 –tan2c )

Trigonometric Identities of half the Angle 

If the angles are reduced to half, then the trigonometric identities for sin, cos and tan are as follow:

sin (C/2) = 1 – cos C2

cos (C/2) = 1 + cos C2

tan (C/2) = 1 – cos C√1+cos C 

Trigonometric Identities of Product-Sum of angles:

The trigonometric identities of Product-Sum of angles change the sum or difference of sin or cos into a product of sin and cos are as follow:

Sin A + Sin B = 2 Sin(A+B)/2 . Cos(A-B)/2

Cos A + Cos B = 2 Cos(A+B)/2 . Cos(A-B)/2

Sin A – Sin B = 2 Cos(A+B)/2 . Sin(A-B)/2

Cos A – Cos B = -2 Sin(A+B)/2 . Sin(A-B)/2

Trigonometric Identities of Products of trigonometric ratios:

These are the some of the product identities of trigonometry are:

Sin A. Sin B = [Cos (A – B) – Cos (A + B)]/2

Sin A. Cos B = [Sin (A + B) – Sin (A – B)]/2

Cos A. Cos B = [Cos (A + B) – Cos (A – B)]/2

CONCLUSION:

Trigonometry is one of the important and powerful tools of mathematics by which we can solve daily life problems like height and distance problems etc. The concept of trigonometry is widely used in different fields like in games, astronomy, space work etc.