A trigonometric function is simply the function of the angle of a right-angled triangle. It is also known to be a circular function. We can find the relationship between the ratio of sides of a triangle to the corresponding angles using these functions.
There are six fundamental functions of trigonometry having an input domain value ‘theta,’ angle of the triangle. We will understand the concept of trigonometry, ratios, their variation in four different quadrants, identities, and graphs.
What are Trigonometric Functions?
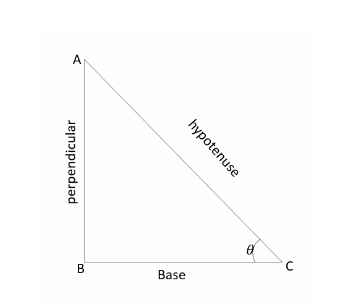
Trigonometric functions are applicable to right-angled triangles. We have three sides in a right-angled triangle: hypotenuse, perpendicular, and base. The ratios of these sides of the triangle give us trigonometric functions. There are six fundamental trigonometric ratios:
- Sine function (sin)
- Cosine function (cos)
- Tangent function (tan)
- Cosecant function (cosec)
- Secant function (sec)
- Cotangent function (cot)


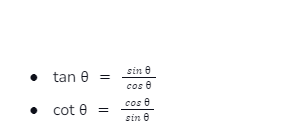
Trigonometric Functions in Four Quadrants
The six trigonometric functions have different signs (negative or positive) in all four quadrants. The angle theta is measured in an anti-clockwise direction taking the x-axis as the principal axis.

The trigonometric functions that get interchanged as their complementary ratios are as follows:
- sin cos
- sec cosec
- tan cot
For the supplementary ratio the functions are not changed. The angle is written as or (90-) in the first quadrant. There is a relation between the cofunction identities. The interrelationship between the angles are given as follows:
- sin (90°-θ) = cosθ
- cos (90°-θ) = sinθ
- sec (90°-θ) = cosecθ
- cosec (90°-θ ) = secθ
- tan (90°-θ) = cotθ
- cot (90°-θ) = tanθ
The domain theta can be written as or (180°- θ) in the second quadrant. Similarly, in the third quadrant, we have the angle as or (180°+θ ) and in the fourth or (270°+θ ). While interchanging the functions, we take the sign as per the functions that we are changing.
For example, sin (90° + θ) =cos θ. Since the second quadrant sine function is positive, we have cos function positive.
Trigonometric Functions Value for Standard Angles
We have some standard angles such as 0, 30°, 45°, 60°, 90°, 180°, 270°, and 360°. In radians, we have the angles as 0, 6 ,4 ,6, 2, , 32, 2 respectively. The values of all the six functions with these standard angles as domains are given in the following table.
0°/ 360° | 30° | 45° | 60° | 90° | |
sin | 0 | 12 | 12 | 32 | 1 |
cos | 1 | 32 | 12 | 12 | 0 |
tan | 0 | 13 | 1 | 3 | ∞ |
cosec | ∞ | 2 | 2 | 23 | 1 |
sec | 1 | 23 | 2 | 2 | ∞ |
cot | ∞ | 3 | 1 | 13 | 0 |
Trigonometric Functions Graphs
For representing the graphs of the trigonometric functions, we take the domain theta on the x-axis and the range on the y-axis.
- For the sine functions, we have domain theta on the x-axis. From the standard angles table, we have the sine function’s range as [-1,1]. Therefore, the graph of the sin function is as follows:
- The range of cos function is also [-1,1]. The graph of the function cos is represented as shown below:
- The graph of a tan function is shown below. Its range is all the real numbers.
- The graph of secant function is shown below; the range is y -1 or y 1.
- The graph of cosecant function with the range as y -1 or y 1 is given below.
- Lastly, we have the cotangent function with the range as all real numbers given below.
Trigonometric Identities
Proceeding further, we have Pythagorean identities. These identities are generated from the Pythagoras theorem. The theorem states that in a right-angled triangle, the sum of squares of two sides of a triangle is equal to the square of its hypotenuse. So, for the triangle given below, we have:
x2+ y2 = z2
Dividing the whole equation by z2
x2z2 + y2z2 = z2z2
(xz)2 + (yz)2 = 1
Now we have:
sin = xz and cos = yz
By substituting these values, we get:
sin²θ + cos²θ = 1
This is the first Pythagorean identity; similarly, we have two more identities:
sec²θ – tan²θ = 1
cosec²θ – cot²θ = 1
Some Other Identities of Trigonometric Functions
Apart from the formulas and identities, we have some other identities of trigonometric functions as well.
1. Angle Sum and Difference Identities
For adding or subtracting trigonometric functions, the formulas are given as follows:
- sin(x±y) = sin(x)±cos(y) cos(x)sin(y)
- cos(x±y) = cos(x)±cos(y) sin(x)sin(y)
- tan(x±y) = (tan x ±tan y)/ (1±tan x tan y)
2. Double Angle Identities
The double angle identities for sin, cos, and tan function are as follows:
- sin 2 = 2 sin cos = 2 tan 1 + tan2
- cos 2 = cos2 – sin2 = 2cos2 – 1 = 1- 2sin2 = 1- tan21+ tan2
- tan 2 = 2 tan 1 – tan2
3. Triangle Identities
Apart from right-angled triangles, trigonometric identities are applicable for all the triangles. These are as follows:
- The Law of Sines
For the triangle above. We have the sine rule as
asin A = bsin B = csin C
Where a, b and c are the lengths of the sides, A, B, and C are the angles.
- The Law of Cosines
The formula gives the cosine rule or law of cosines:
c2 = a2 + b2 – 2ab cos C
It is just the expanded form of the Pythagoras theorem.
- The Law of Tangents
The law of tangent is given as
a + ba – b = tan [12(A + B)]tan [12(A – B)]
Conclusion
Trigonometry is an essential element of mathematics that has made it easier to understand various concepts. It was Hipparchus who first introduced it, and that is why he is known as the Father of Trigonometry. The trigonometric functions are widely used in various fields such as electronics, chemistry, ultrasound, computer graphics, civil engineering, etc.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






