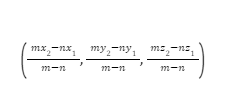Three Dimensional Geometry

Three-dimensional geometry requires the usage of three coordinates, namely, the x-axis, the y-axis, and the z-axis. These coordinates provide the location of the object with respect to the origin on the cartesian plane. In this way, various other properties, such as distance, area, angle, etc., of the object are under observation. Furthermore, three-dimensional geometry covers the analytical mathematics to represent the objects around us in the best possible way and increase the efficiency of their architectural design and development. The representation of objects in 3D has various applications in real-life.

The Three Dimensional Geometry Cartesian Plane

For three dimensional geometry, 3 mutually perpendicular lines (x-axis, y-axis, and z-axis) are used. These axes intersect at a point that represents the observer and is termed as O. This cartesian plane helps to locate any three-dimensional object with the help of its coordinates or the angle that it makes along any coordinate.

• The origin, O, is the base point from where all the coordinate values are calculated while measuring the distance.
• The upper part of the y-axis, the right side of the x-axis, and the outer part of the z-axis, from the origin, have a positive sign.
• The lower part of the y-axis, the left side of the x-axis, and the inward part of the z-axis, from the origin, have a negative sign.
• The sign conventions should be considered carefully as they provide the exact position and geometry of the three-dimensional object.
• The three-dimensional geometry represents a complex coordinate system which is also referred to as the rectangular coordinate system.
• It considers the arithmetic, analytical, and algebraic rules before locating any object and for calculation of its properties for architectural purposes.

The study material notes on three-dimensional geometry provide various theorems and applications to calculate the relative and exact position of the objects.

Evaluating Distance of a Point from Origin

The basic application of three-dimensional geometry is the calculation of the distance of a point from the origin. This helps to calculate the length of the sides of an object by providing a basic idea about the distance calculation technique in the cartesian plane.

• Let’s consider a point K with coordinates (m,n,p) on the cartesian plane where m, n, and p represent the values of the point on the x-axis, the y-axis, and the z-axis respectively.
• As there is only one point, its distance from the origin will be considered where origin has the coordinates (0,0,0)
• The distance of the point K from origin is given by d = ((0-m)2 + (0-n)2+ (0-p)2)1/2
• Hence, d = (m2 + n2 + p2))1/2

Three Dimensional Geometry for Representation of Two Points

In a cartesian plane, the two points can be represented with the help of their coordinates, and this helps to calculate the distance between these two points. Also, if a point internally divides the line segment formed by these two points, the ratio of the division of the line segment can be calculated.

• Let’s take two points, S and K, with coordinates (m1, n1, p1) and (m2, n2, p2) respectively, where the points m1 and m2 represent the x-coordinates, n1 and n2 represent the y-coordinates, and p1 and p2 represent the z-coordinates of points S and K respectively.
• To find the distance between the two points S and K, the procedure is similar to that of calculating the distance of a point from the origin.
• Instead of taking the coordinates of the origin, the coordinates of the other point are taken.
• Therefore, the formula of calculating the distance between the two points is given by d = ((m1-m2)2 + (n1-n2)2 + (p1-p2)2)1/2

• Let’s take a point R with coordinates (m3, n3, p3) where m3, n3, and p3   represent the x-coordinate, the y-coordinate, and the z-coordinate, respectively. 
• If point R internally divides the line segment formed by points S and K in the ratio of a:b, the coordinates of R can be calculated.
• In this case, m3 = (am2 + bm1)/(a+b), n3 = (an2 + bn1)/(a+b), and p3 = (ap2 + bp1)/(a+b)

Three Dimensional Geometry and Cosine Relation

The cosine of an angle and the three-dimensional geometry are related. Let’s consider two points, S and R making a line segment. A line segment in three-dimensional geometry can make three angles with each coordinate.

• Let’s take the angle formed by the line segment SR be m, n, and p with the x-axis, the y-axis, and the z-axis respectively.
• Hence, the cosine of these angles will be cos(m), cos(n), and cos(p). Let’s represent these cosines, i.e., cos(m), cos(n), and cos(p) with a, b, and c respectively.
• The direction cosines of a line have the relationship, a2 + b2 + c2 = 1
• Let’s take the coordinates of points S and R be (u1, v1, w1) and (u2, v2, w2)
• Also, the direction cosines of a line that intersects the line segment formed by SR are given by (u2- u1)/(((u2 – u1)2 + (v2 – v1)2 + (w2- w1)2)1/2), (v2 – v1)/(((u2 – u1)2 + (v2 – v1)2 + (w2 – w1)2)1/2), (w2- w1)/(((u2 – u1)2 + (v2 – v1)2 + (w2- w1)2)1/2

Measuring Angle formed by Two Lines in Three Dimensional Geometry

If there are two lines and the angle formed by them has to be found, the cosines of these two lines are required.

• Suppose there are two lines, SK and SR, with cosines (a1, b1, c1) and (a2, b2, c2), respectively.
• Let’s denote the angle between these two by l.
• Then, the value of l = cos-1(a1a2 + b1b2 + c1c2).

Conclusion

Three-dimensional geometry is a complex yet interesting topic as it deals with real-life objects with varying shapes consisting of curves with complex representations. The mathematical concept is widely used in the architectural domain. It requires the calculation of areas, associated angles, cosine ratios, and other trigonometric functions associated with the three-dimensional object. Using this, any object can be structured, modified, and represented using a plane that makes the communication of ideas and architectural plans easier.