The fundamental theorem of calculus is a theorem that connects the concepts of differentiating and integrating functions (calculating the gradient) (calculating the area under the curve). Apart from a fixed value that is depending on where one begins to compute area, the two processes are inverses of each other.
The first portion of the theorem, which is also known as the first fundamental theorem of calculus, states that one of the antiderivatives (also known as an indefinite integral) of a function, say F, can be found as the integral of a variable bound of integration. For continuous functions, this implies the presence of antiderivatives.
The second half of the theorem, known as the second fundamental theorem of calculus, on the other hand, the integral of a function f over some interval can be computed using any of its infinitely numerous antiderivatives, such as F. This aspect of the theorem is useful in practice since it avoids using numerical integration to compute integrals by explicitly calculating the antiderivative of a function via symbolic integration.
Geometric Meaning
Each value of x has a corresponding area function A(x), which is the area beneath the curve between 0 and x for a continuous function y = f(x) whose graph is represented as a curve. Although the function A(x) is unknown, it is known to represent the area under the curve.
Finding the area between 0 and x + h, then subtracting the area between 0 and x, yields the area under the curve between x and x + h. To put it another way, the area of this “strip” is A(x + h) – A (x). There’s another way to figure out how big this strip is. h is multiplied by f(x) to find the area of a rectangle that is roughly the same size as this strip, as shown in the following picture. So:
A(x+h) – A(x)≈ f(x).h
A(x+h)-A(x)≈f(x).h
When we include the red section of the “extra” region depicted in the diagram, this estimate becomes complete equality. So:
A(x+h)-A(x)=f(x).h + (Red excess)
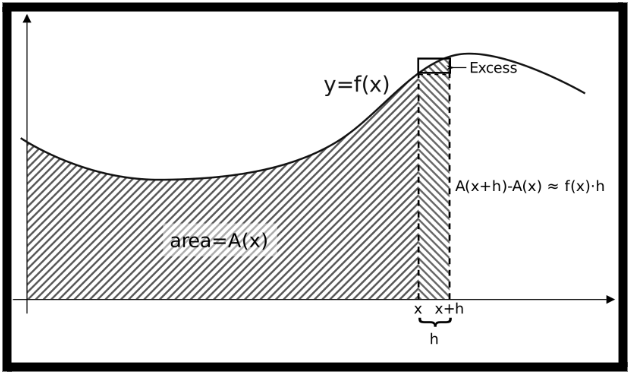
Rearranging the term, we get
The last fraction may be shown to go to zero as h approaches 0 in the limit. [6] This is because the red component of the excess region has a smaller or equal area than the little black-bordered rectangle. Specifically,
where x+h1 and x+h2 are the places in the interval [x, x + h] where f achieves its maximum and lowest, respectively. The latter term, like h, tends to zero due to the continuity of f. As a result, the left-hand side tends to zero, just as h does, implying
This means that f(x) = A′. (x). That is, the area function A(x) has a derivative, which is the original function f(x); thus, the area function is simply the antiderivative of the original function. Finding the area under a curve and computing the derivative of a function are “opposite” processes. The Fundamental Theorem of Calculus boils down to this.
Formal Statement
The theorem is divided into two sections. The derivative of an antiderivative is covered in the first section, while the relationship between antiderivatives and definite integrals is covered in the second.
The first section
The first fundamental theorem of calculus is commonly referred to as this section.
Let f be a closed interval continuous real-valued function defined on [a, b]. Let F be the function defined by [a, b] for every x.
Then F is differentiable on the open interval (a, b) and uniformly continuous on [a, b], and
F'(x)=f(x)
For all x in (a, b), F'(x)=f(x), hence F is an antiderivative of function f.
Corollary
The fundamental theorem is frequently used to find the definite integral of a function f that has an antiderivative F. If f is a continuous real-valued function on [a, b] and F is an antiderivative of f in [a, b], then
The corollary assumes that the interval is continuous throughout. The following section of the theorem strengthens this result slightly.
Second part
This section is also known as the Newton–Leibniz axiom or the second fundamental theorem of calculus.
Let f be a real-valued function on a closed interval, and F be the antiderivative of f in (a, b):
F'(x)=f(x).
If f on [a, b] is Riemann integrable, then
Because it does not presuppose that f is continuous, the second component is more powerful than the corollary.
When an antiderivative of f exists, there are an infinite number of antiderivatives for f that may be generated by adding an arbitrary constant to F. Antiderivatives of f always exist when f is continuous, according to the first half of the theorem.
Conclusion
The FTC came to the key conclusion that if you integrate f first and then differentiate the result, you come back to f:
(The functions f(t) and f(x) are the same, but the independent variables are different.) On [a, b], f must be continuous. The integral can be found–without finding the integral–as long as the problem matches this form. Remember that if the variable of differentiation is the lower limit and the constant is the higher limit in the given problem, flip the limits and multiply by a. (-1). Also, if the supplied problem has an upper limit function, try making it equal to u, getting the answer, and inserting du/dx, finding du, which then finds du/dx and substitute back.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






