Profile
Settings
Refer your friends
Sign out
The binomial theorem provides a formula to expand the algebraic statement (x+y)^n to a sum of terms, using individual exponents of variables x and y. The expanded value of these algebraic expressions is determined by using this theorem. It is easy to calculate the value of expressions such as (x + y + z)^6, (a + b) ^5, and so on, by multiplying the number of times by the exponent value. The binomial theorem, on the contrary, can also be used to find the expanded version of (x+y)^17 or another expression with the largest exponential values.
Binomial expansion is given as:
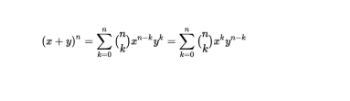
Example of Binomial Theorem
Consider the following expansion:
(x+y)4=x4+4x3y+6x2y2+4xy3+y4
Any coefficient a in the term axbyc of the expanded version is called the binomial coefficient. This binomial coefficient also occurs in combinatorics where it provides many different combinations of ‘b’ elements that can be selected from a set of ‘n’ elements. Recall that it could also be written as (nb)(nb) or ‘n’ choose ‘b’.
Binomial Expansion Terms
The binomial expansion terms using the binomial theorem are listed below. Here are the specifics of each of the terms:
General Term
The General term represents all the terms in the (x + y)n binomial expansion. The general term in the binomial expansion of (x + y)n is Tr+1=nCrxn-ryr. The r-value is one less than the number of terms of the binomial expansion. In this case, nCris the coefficient. Also, the sum of exponents of the x and y variables is equal to n.
Middle Term
The total number of terms in the (x + y)^n expansion is equal to n + 1. The value of ‘n’ determines the middle term in the binomial expansion. The total number of terms and the value of ‘n’ rely on whether n is an odd number or an even number. For an even value of n, there is only one middle term, which is the (n/2 + 1)th term. There are two middle terms for an odd number of n, and they are n/2 and n/2 +1.
Identifying a particular term
It takes two steps to identify a certain term containing xp. The first step involves finding the general term in the expansion of (x + y)n, which is Tr+1=nCr xn-ryr. In the second step, we need to compare the expanded value with xp to find the value of r. The value of r helps in obtaining the particular term.
Term Independent of x
Finding a term independent of x follows the same method as finding a specific term in the binomial expansion. We need to first find the general term in the expansion of (x + y)n. which is Tr+1=nCr xn-ryr. To find a term independent of x, we must discover and equalise the exponents of x in the general term to 0. The term independent of x is the (r + 1)th term, which is derived from the obtained value of r.
Numerically greatest term
The formula to find the numerically greatest term in the expansion of(1 + x)n is (n+1)|x|/1+|x|. Two points need to be remembered while using this formula to find the numerically greatest term. First we need to convert any Binomial expansion into the form of (1 + x)nn. We can convert (2x + 3y)5 to (1 + 3y/2x)5. Further, for this expansion, |x| is the numeric value, which in this case is 3/2. To obtain the numerically biggest term, the final result is rounded to the integral value.
Binomial Theorem coefficients
In the expansion of (x + y)^n, the binomial coefficients are the numbers associated with the variables x, y in the expansion of (x + y)n. The binomial coefficients are represented as nC0, nC1, nC2….. nCr. The pascal triangle or the combinations formula are used to calculate the binomial coefficients.
Conclusion
The binomial theorem is one of the most used formulas in mathematics. It is used to answer problems in data science and finds its most significant use in statistics and probability analysis. In advanced mathematics and computing, the Binomial Theorem is used to find the roots of equations with advanced powers. Many substantial physics and calculi equations are also validated using it. The binomial theorem is extensively used in weather forecasting services, architecture, and cost estimation in engineering systems.
