Tangents and Their Associated Properties

A tangent is a line in geometry that is drawn from an external point and passes through a point on a curve. Every point on the circle of the wheel forms a tangent with the road when cycling. This is an example of a possible tangent in real life. First, let’s examine a specific example of the tangent concept. The diagram below depicts a point P that is placed outside of the arc S. P has been used as the starting point for a tangent to S. This is an example of how a tangent could be expressed.

Tangent Definition

In geometry, a line is a tangent to a curve or surface if it touches the curve or surface at exactly one point. This definition is derived from the study of geometry.

Point of Tangency

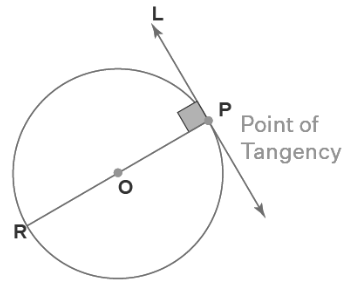
The point at which a straight line meets or enters a circle is known as the point of tangency, and it is defined as the intersection of the two lines. Point P in the figure just provided represents the tangency point.

A Point on the Circular Margin

A tangent of a circle can be defined as a straight line that meets or intersects the circle at precisely one point. Chords are also known as tangents. A tangent is a line that touches the circumference of a circle but does not penetrate its interior. The subsequent diagram depicts a circle with a point designated by P. It has been established that tangent L passes through point P. Here is an illustration of a tangent to a circle.

Tangent Properties

The most important tangent features are as follows:

• A tangent intersects a curve at precisely one location.
• A tangent is a line that never penetrates the circle’s interior.
• At the point of tangency, the tangent makes a right-angle contact with the circle’s radius.

There are mathematical theorems associated with tangents to circles, and these theorems are utilised in geometry’s most complex computations. In addition to the characteristics listed previously, these theorems can be found here.

Available Tangent Types

The following is a list of types of tangents:

Fixed

The Fixed tangent type does not alter the existing control points, but they no longer update when keyframes are changed around them. Once a tangent has been manually moved, this type becomes the tangent type.

Flat

The Flat tangent type positions the control points on either side of the keyframe horizontally. Each keyframe uses the Flat tangent type.

Linear

The Linear tangent type aligns the control point directly with the keyframe that serves as the segment’s other anchor point. If both control points for a bezier segment are linear, the segment from one keyframe to the next is a straight line. The first and second keyframes use the linear tangent, but the third keyframe does not.

Smooth

The Smooth tangent type positions the control points on either side of a keyframe to generate a line parallel to the line created by the keyframes on either side. The line generated by the control points continues to be parallel to the line produced by the keyframes.

Smooth Normal

The Smooth Normal tangent type positions the two control points along the keyframe’s vertical axis. Whichever keyframe is higher between the left and right keyframes controls the direction of the curve. Should the left and right keyframes be equal, both control points are positioned vertically below.

Plateau

The Plateau tangent type utilises the Flat and Smooth tangent types based on the relative position of its keyframes to the keyframes on either side. If the keyframes on both sides are above or below the tangent’s keyframe, the Flat tangent type is utilised. If the keyframe of the tangent lies between the values of the keyframes on either side, the Smooth tangent type is utilised. If one of the tangent’s control points would fall beyond the range between the keyframes on either side while using the Smooth tangent type, that control point is converted to the Flat tangent type instead.

Constructing a Circle Tangent

Step 1: From the circle’s centre, draw a straight line through the provided point on the circle’s perimeter or outside the circle. Ensure that the line goes far beyond the circle’s perimeter.

Step 2: Determine where the line you just drew intersects with the circle. Then, draw two points on the line, one on the inside and one on the outside of the circle, that is equally distant from the intersection point.

Step 3: Using a compass and each of the two equidistant points, draw a circle around each point. The radius of each circle must be greater than the distance between the point and the intersection of the line and the circle.

Step 4: Identify the two points where the circles intersect and draw a line between them. This line will be tangent to the circle in every way.

Tangent Examples in Real Life

When riding a bicycle along a road, the road becomes the tangent at each point where the wheels ride on it, because the road moves with the bicycle.

Conclusion

This article discussed how a line is regarded as a tangent to a circle if it only touches the circle’s circumference at a single point. The addition of real-world examples considerably enhances the capacity to relate to the concept. In addition, we discussed the properties of the tangent to a circle, such as the number of tangents that may be formed from a point inside, on, or outside the circle.